Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре и начала математического анализа 11 класс Алимов Задание 332
Задание 332
\[\boxed{\mathbf{332}\mathbf{.}}\]
\[1)\ y = \log_{3}(x - 1)\]
\[y = \log_{3}x:\]
\[\ Область\ определения:\ \ x > 0.\]
\[Множество\ значений:\ \ y \in R.\]
\[Функция\ возрастает,\ \]
\[так\ как\ 3 > 1.\]
\[Построим\ график\ функции\ \]
\[y = \log_{3}x\ и\ осуществим\ его\ \]
\[сдвиг\ вдоль\ оси\ абсцисс\ \]
\[на\ 1\ единицу\ вправо:\]
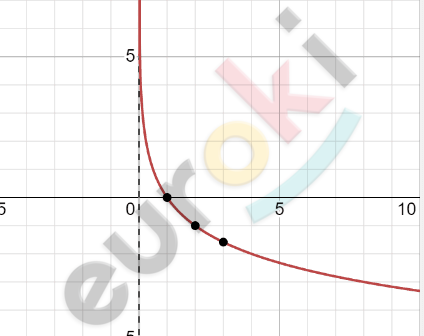
\[Ответ:\ \ D(x) = (1;\ + \infty);\ \ \]
\[E(y) = ( - \infty;\ + \infty).\]
\[2)\ y = \log_{\frac{1}{3}}(x + 1)\]
\[\ y = \log_{\frac{1}{3}}x:\]
\[Область\ определения:\ \ x > 0.\]
\[Множество\ значений:\ \ y \in R.\]
\[Функция\ убывает,\ \]
\[так\ как\ 0 < \frac{1}{3} < 1.\]
\[Построим\ график\ функции\ \]
\[y = \log_{\frac{1}{3}}x\ и\ осуществим\ его\ \]
\[сдвиг\ вдоль\ оси\ абсцисс\ \]
\[на\ 1\ единицу\ влево:\]
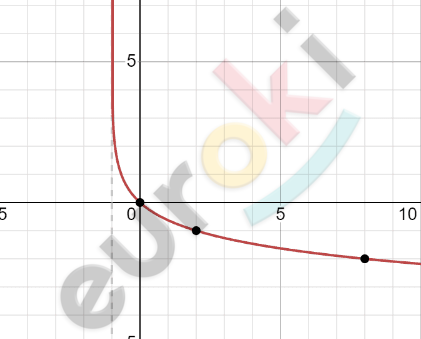
\[Ответ:\ \ D(x) = ( - 1;\ + \infty);\ \ \]
\[E(y) = ( - \infty\ ; + \infty).\]
\[3)\ y = 1 + \log_{3}x\]
\[y = \log_{3}x:\]
\[Область\ определения:\ \ x > 0.\]
\[Множество\ значений:\ \ y \in R.\]
\[Функция\ возрастает,\ \]
\[так\ как\ 3 > 1.\]
\[Построим\ график\ функции\ \]
\[y = \log_{3}x\ и\ осуществим\ его\ \]
\[сдвиг\ вдоль\ оси\ ординат\ \]
\[на\ 1\ единицу\ вверх:\]
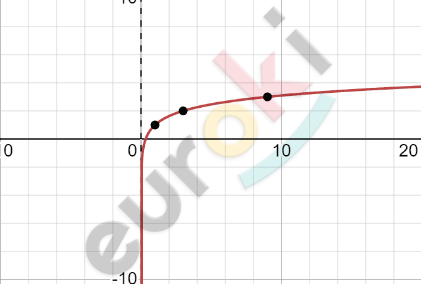
\[Ответ:\ \ D(x) = (0;\ + \infty);\ \ \]
\[E(y) = ( - \infty;\ + \infty).\]
\[4)\ y = \log_{\frac{1}{3}}x - 1\]
\[y = \log_{\frac{1}{3}}x:\]
\[Область\ определения:\ \ x > 0.\]
\[Множество\ значений:\ \ y \in R.\]
\[Функция\ убывает,\ \]
\[так\ как\ 0 < \frac{1}{3} < 1.\]
\[Построим\ график\ функции\ \]
\[y = \log_{\frac{1}{3}}x\ и\ осуществим\ его\ \]
\[сдвиг\ вдоль\ оси\ ординат\ \]
\[на\ 1\ единицу\ вниз:\]
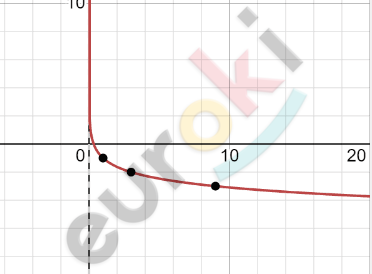
\[Ответ:\ \ D(x) = (0;\ + \infty);\ \ \]
\[E(y) = ( - \infty;\ + \infty).\]
\[5)\ y = 1 + \log_{3}(x - 1)\]
\[y = \log_{3}x:\]
\[Область\ определения:\ \ x > 0.\]
\[Множество\ значений:\ \ y \in R.\]
\[Функция\ возрастает,\ \]
\[так\ как\ 3 > 1.\]
\[Построим\ график\ функции\ \]
\[y = \log_{3}x\ и\ осуществим\ его\ \]
\[сдвиг\ вдоль\ оси\ абсцисс\ \]
\[на\ 1\ единицу\ вправо\ и\ вдоль\ \]
\[оси\ ординат\ на\ 1\ единицу\]
\[вверх:\]
\[Ответ:\ \ D(x) = (1;\ + \infty);\ \ \]
\[E(y) = ( - \infty;\ + \infty).\]
