ГДЗ > 📚 Алгебра > 11 класс > 📗 Алгебра и начала математического анализа 11 класс Алимов, Колягин > 🧠 Задание 237

Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 237

Авторы:
Год:2020-2021-2022-2023
Тип:учебник
Серия:Алгебра и начала математического анализа, геометрия

Задание 237

\[\boxed{\mathbf{237}\mathbf{.}}\]

\[1)\ 2^{x} = 3 - 2x - x^{2}\]

\[y = 2^{x} - показательная\ \]

\[функция.\]

\[x\] \[0\] \[1\] \[2\]
\[y\] \[1\] \[3\] \[9\]

\[y = 3 - 2x - x^{2} - уравнение\ \]

\[параболы.\]

\[x_{0} = - \frac{b}{2a} = - \frac{- 2}{- 2} = - 1\ \]

\[\text{\ \ }y_{0} = 3 + 2 - 1 = 4.\]

\[x\] \[- 4\] \[- 3\] \[- 2\] \[0\] \[1\] \[2\]
\[y\] \[- 5\] \[0\] \[3\] \[3\] \[0\] \[- 5\]

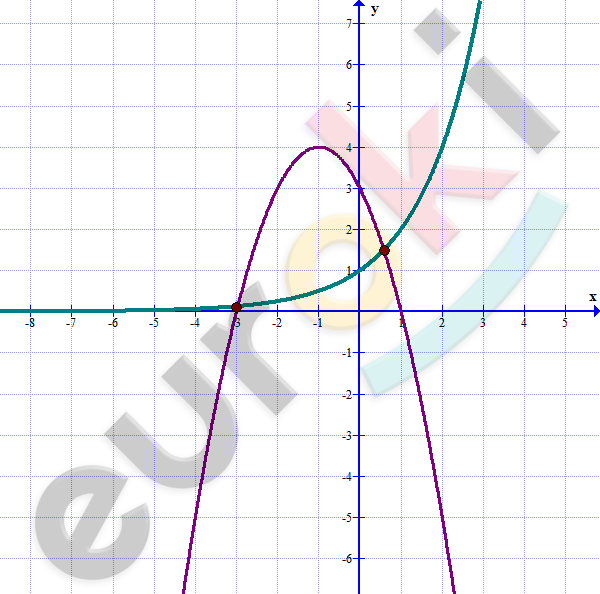
\[Ответ:\ \ x_{1} \approx - 3\ \ \ x_{2} \approx 0,6.\]

\[2)\ 3^{- x} = \sqrt{x}\]

\[y = 3^{- x} = \left( \frac{1}{3} \right)^{x} -\]

\[показательная\ функция.\]

\[x\] \[- 2\] \[- 1\] \[0\]
\[y\] \[9\] \[3\] \[1\]

\[y = \sqrt{x} - уравнение\ ветви\ \]

\[параболы.\]

\[x \geq 0\ \text{\ \ }y \geq 0.\]

\[x\] \[0\] \[1\] \[4\] \[9\]
\[y\] \[0\] \[1\] \[2\] \[3\]

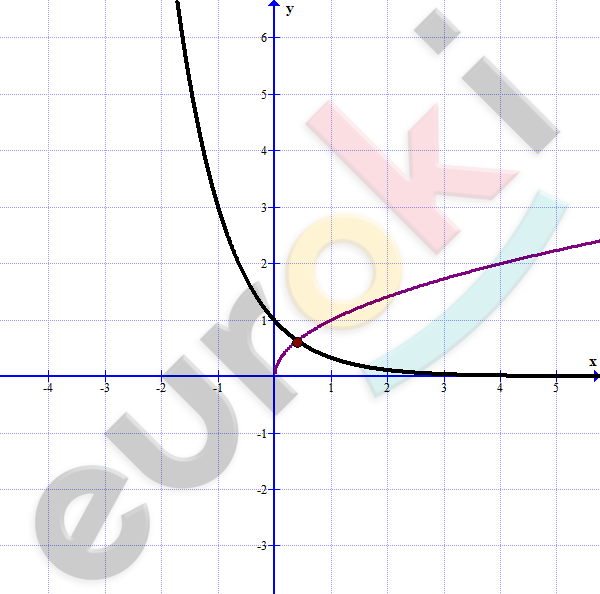
\[Ответ:\ \ x \approx 0,4.\]

\[3)\ \left( \frac{1}{3} \right)^{x} = - \frac{3}{x}\]

\[y = \left( \frac{1}{3} \right)^{x} - показательная\ \]

\[функция.\]

\[x\] \[- 2\] \[- 1\] \[0\]
\[y\] \[9\] \[3\] \[1\]

\[y = - \frac{3}{x} - уравнение\ \]

\[гиперболы.\]

\[x \neq 0\ \text{\ \ }y \neq 0.\]

\[x\] \[- 3\] \[- 1\] \[1\] \[1\]
\[y\] \[1\] \[3\] \[- 3\] \[1\]

\[Ответ:\ \ x = - 1.\]

\[4)\ \left( \frac{1}{2} \right)^{x} = x^{3} - 1\]

\[y = \left( \frac{1}{2} \right)^{x} - показательная\ \]

\[функция.\]

\[x\] \[- 3\] \[- 2\] \[- 1\] \[0\]
\[y\] \[8\] \[4\] \[2\] \[1\]

\[y = x^{3} - 1 - уравнение\ \]

\[кубической\ параболы.\]

\[x_{0} = 0\ \]

\[\text{\ \ }y_{0} = 0^{3} - 1 = - 1.\]

\[x\] \[- 2\] \[- 1\] \[1\] \[2\]
\[y\] \[- 9\] \[- 2\] \[0\] \[7\]

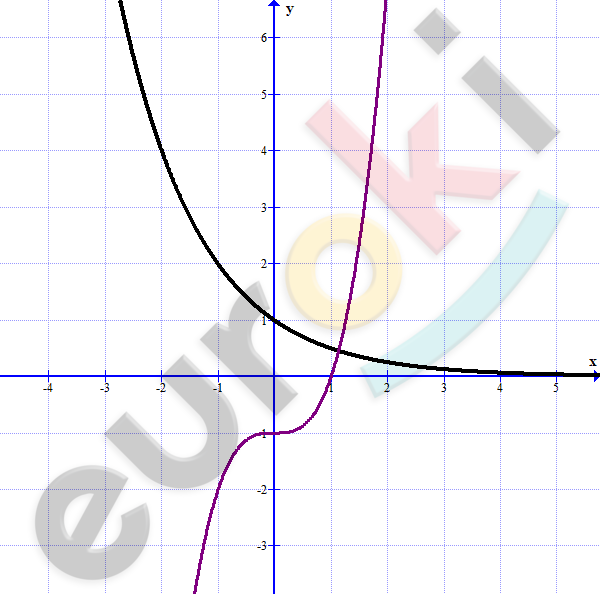
\[Ответ:\ \ x \approx 1,1.\]

Скачать ответ
Есть ошибка? Сообщи нам!

237
Решебники по другим предметам