Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре и начала математического анализа 11 класс Алимов Задание 163
Задание 163
\[\boxed{\mathbf{163.}}\]
\[1)\ \sqrt{4x + 2\sqrt{3x^{2} + 4}} = x + 2\]
\[4x + 2\sqrt{3x^{2} + 4} = x^{2} + 4x + 4\]
\[2\sqrt{3x^{2} + 4} = x^{2} + 4\]
\[4\left( 3x^{2} + 4 \right) = x^{4} + 8x^{2} + 16\]
\[12x^{2} + 16 = x^{4} + 8x^{2} + 16\]
\[x^{4} - 4x^{2} = 0\]
\[x^{2} \bullet \left( x^{2} - 4 \right) = 0\]
\[(x + 2) \bullet x^{2} \bullet (x - 2) = 0\]
\[x_{1} = - 2,\ \ \ x_{2} = 0,\ \ \ x_{3} = 2.\]
\[Проверим:\]
\[\sqrt{- 2 \bullet 4 + 2\sqrt{3 \bullet 4 + 4}} + 2 =\]
\[= \sqrt{- 8 + 2\sqrt{16}} + 2 =\]
\[= \sqrt{0} + 2 = 2;\]
\[\sqrt{2 \bullet 4 + 2\sqrt{3 \bullet 4 + 4}} - 2 =\]
\[= \sqrt{8 + 2\sqrt{16}} - 2 =\]
\[= \sqrt{16} - 2 = 2;\]
\[\sqrt{4 \bullet 0 + 2\sqrt{3 \bullet 0^{2} + 4}} - 0 =\]
\[= \sqrt{2\sqrt{4}} = \sqrt{4} = 2.\]
\[Ответ:\ \ x = \pm 2;\ \ x = 0.\]
\[2)\ 3 - x = \sqrt{9 - \sqrt{36x^{2} - 5x^{4}}}\]
\[9 - 6x + x^{2} = 9 - \sqrt{36x^{2} - 5x^{4}}\]
\[x^{2} - 6x = - \sqrt{36x^{2} - 5x^{4}}\]
\[x^{4} - 12x^{3} + 36x^{2} = 36x^{2} - 5x^{4}\]
\[6x^{4} - 12x^{3} = 0\]
\[x^{4} - 2x^{3} = 0\]
\[x^{3} \bullet (x - 2) = 0\]
\[x_{1} = 0;\ \ \ x_{2} = 2.\]
\[Проверим:\]
\[\sqrt{9 - \sqrt{36 \bullet 0^{2} - 5 \bullet 0^{4}}} + 0 =\]
\[= \sqrt{9 - \sqrt{0}} = 3;\]
\[\sqrt{9 - \sqrt{36 \bullet 2^{2} - 5 \bullet 2^{4}}} + 2 =\]
\[= \sqrt{9 - \sqrt{64}} + 2 = \sqrt{1} + 2 = 3.\]
\[Ответ:\ \ x = 0;\ \ x = 2.\]
\[3)\ \sqrt{x^{2} + 3x + 12} - \sqrt{x^{2} + 3x} =\]
\[= 2\]
\[\sqrt{x^{2} + 3x + 12} = 2 + \sqrt{x^{2} + 3x}\]
\[x^{2} + 3x + 12 =\]
\[= 4 + 4\sqrt{x^{2} + 3x} + x^{2} + 3x\]
\[8 = 4\sqrt{x^{2} + 3x}\]
\[2 = \sqrt{x^{2} + 3x}\]
\[4 = x^{2} + 3x\]
\[x^{2} + 3x - 4 = 0\]
\[D = 3^{2} + 4 \bullet 4 = 9 + 16 = 25\]
\[x_{1} = \frac{- 3 - 5}{2} = - 4;\ \ \ \]
\[x_{2} = \frac{- 3 + 4}{2} = 1.\]
\[Проверим:\]
\[\sqrt{16 - 3 \bullet 4 + 12} - \sqrt{16 - 3 \bullet 4} =\]
\[= \sqrt{16} - \sqrt{4} = 4 - 2 = 2;\]
\[\sqrt{1 + 3 + 12} - \sqrt{1 + 3} =\]
\[= \sqrt{16} - \sqrt{4} = 4 - 2 = 2.\]
\[Ответ:\ \ x_{1} = - 4;\ \ x_{2} = 1.\]
\[6 = 2\sqrt{x^{2} + 5x + 3}\]
\[3 = \sqrt{x^{2} + 5x + 3}\]
\[9 = x^{2} + 5x + 3\]
\[x^{2} + 5x - 6 = 0\]
\[D = 5^{2} + 4 \bullet 6 = 25 + 24 = 49\]
\[x_{1} = \frac{- 5 - 7}{2} = - 6;\text{\ \ }\]
\[x_{2} = \frac{- 5 + 7}{2} = 1.\]
\[Проверим:\]
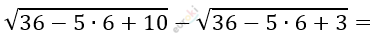
\[= \sqrt{16} - \sqrt{9} = 4 - 3 = 1;\]
\[\sqrt{1 + 5 + 10} - \sqrt{1 + 5 + 3} =\]
\[= \sqrt{16} - \sqrt{9} = 4 - 3 = 1.\]
\[Ответ:\ \ x_{1} = - 6;\ \ x_{2} = 1.\]
