Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 164

\[\boxed{\mathbf{164.}}\]

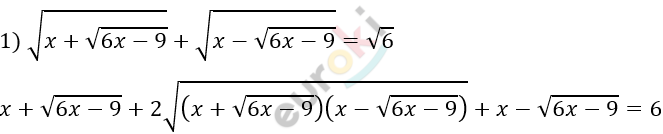
\[2\sqrt{x^{2} - (6x - 9)} = 6 - 2x\]

\[\sqrt{x^{2} - 6x + 9} = 3 - x\]

\[x^{2} - 6x + 9 = 9 - 6x + x^{2}\]

\[0x = 0 - при\ любом\ x.\]

\[Выражение\ имеет\ смысл\ при:\]

\[6x - 9 \geq 0\]

\[6x \geq 9\]

\[x \geq 1,5.\]

\[Выражение\ имеет\ смысл\ при:\]

\[x - \sqrt{6x - 9} \geq 0\]

\[x \geq \sqrt{6x - 9}\]

\[x^{2} \geq 6x - 9\]

\[x^{2} - 6x + 9 \geq 0\]

\[(x - 3)^{2} \geq 0 - при\ любом\ x.\]

\[Уравнение\ имеет\ решения\ при:\]

\[6 - 2x \geq 0\]

\[3 - x \geq 0\]

\[x \leq 3.\]

\[Ответ:\ \ 1,5 \leq x \leq 3.\]

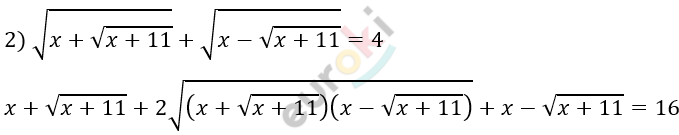
\[2\sqrt{x^{2} - (x + 11)} = 16 - 2x\]

\[\sqrt{x^{2} - x - 11} = 8 - x\]

\[x^{2} - x - 11 = 64 - 16x + x^{2}\]

\[15x = 75\]

\[x = 5.\]

\[Проверим:\]

\[\sqrt{5 + \sqrt{5 + 11}} + \sqrt{5 - \sqrt{5 + 11}} =\]

\[= \sqrt{5 + \sqrt{16}} + \sqrt{5 - \sqrt{16}} =\]

\[= \sqrt{9} + \sqrt{1} = 4.\]

\[Ответ:\ \ x = 5.\]