Знаменатель обыкновенной дроби на 11 больше её числителя. Если числитель этой дроби увеличить на 1, а знаменатель уменьшить на 2, то полученная дробь будет на 1/9 больше исходной. Найдите исходную дробь.

\[Пусть\ x - числитель\ дроби;\ \ \]

\[(x + 11) - ее\ знаменатель.\]

\[x + 1 - новый\ числитель\ \]

\[дроби;\]

\[x + 11 - 2 = x + 9 - новый\ \]

\[знаменатель.\]

\[Известно,\ что\ полученная\ \]

\[дробь\ на\ \frac{1}{9}\ больше\ исходной.\]

\[Составим\ уравнение:\ \ \]

\[\frac{x}{x + 11} = \frac{x + 1}{x + 11 - 2} - \frac{1}{9}\]

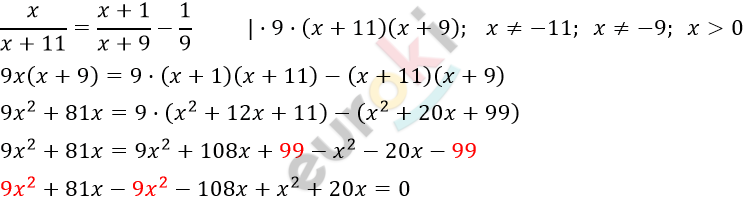
\[x^{2} - 7x = 0\]

\[x(x - 7) = 0\]

\[x = 0\ (не\ подходит).\]

\[x - 7 = 0\ \ \]

\[x = 7 - числитель\ дроби.\]

\[x + 11 = 7 + 11 =\]

\[= 18 - знаменатель\ дроби.\]

\[Ответ:\ \frac{7}{18} - исходная\ дробь.\]