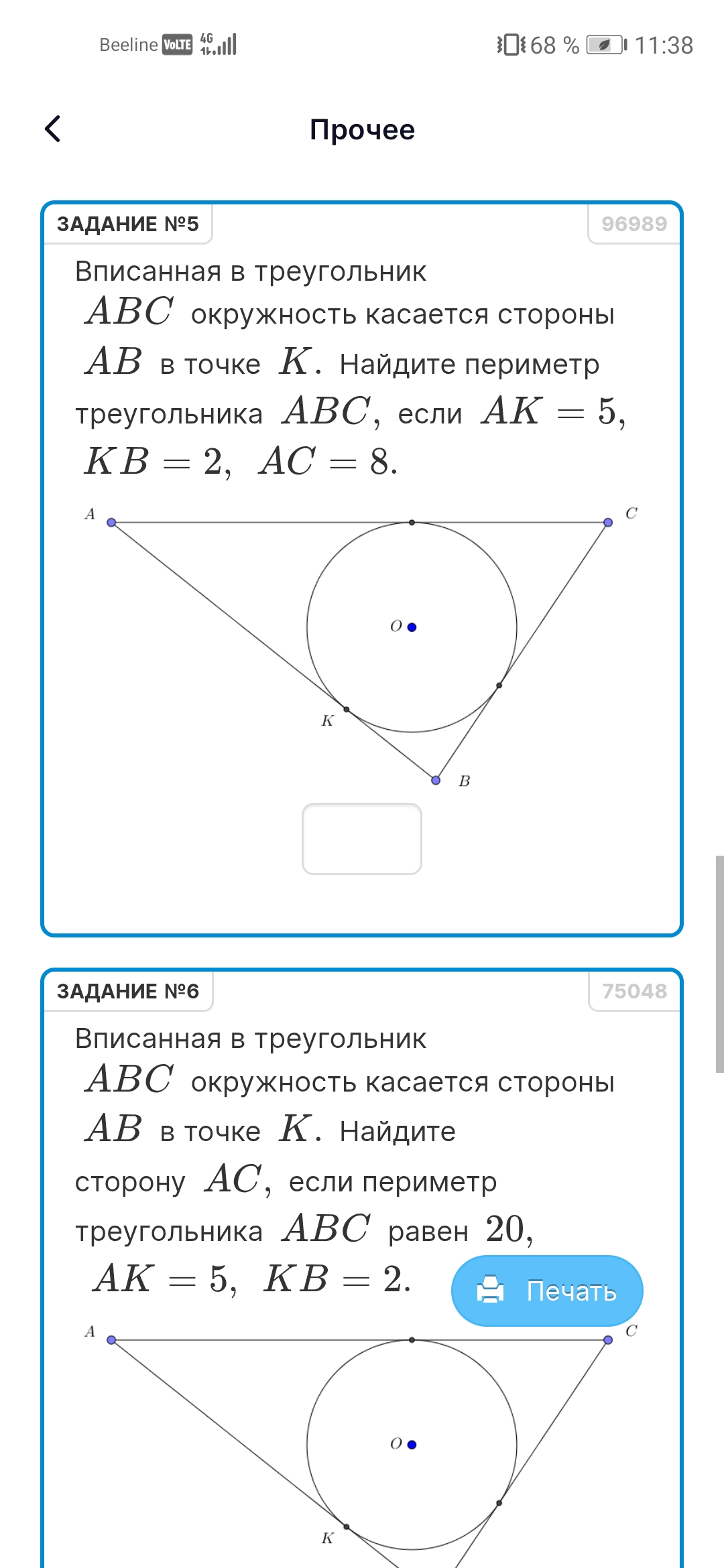
ЗАДАНИЕ №6: Вписанная в треугольник ABC окружность касается стороны AB в точке K. Найдите сторону AC, если периметр треугольника ABC равен 20, AK = 5, KB = 2.

Аналогично предыдущей задаче, обозначим точки касания окружности со сторонами BC и AC как M и N соответственно. По свойству касательных, AK = AN = 5, KB = BM = 2, и CM = CN. AB = AK + KB = 5 + 2 = 7. Периметр треугольника ABC равен P = AB + BC + AC = 20. BC = BM + MC = 2 + CM. AC = AN + NC = 5 + CN = 5 + CM. Тогда P = AB + BC + AC = 7 + (2 + CM) + (5 + CM) = 20. 14 + 2 * CM = 20. 2 * CM = 6. CM = 3. AC = 5 + CM = 5 + 3 = 8. Ответ: 8.