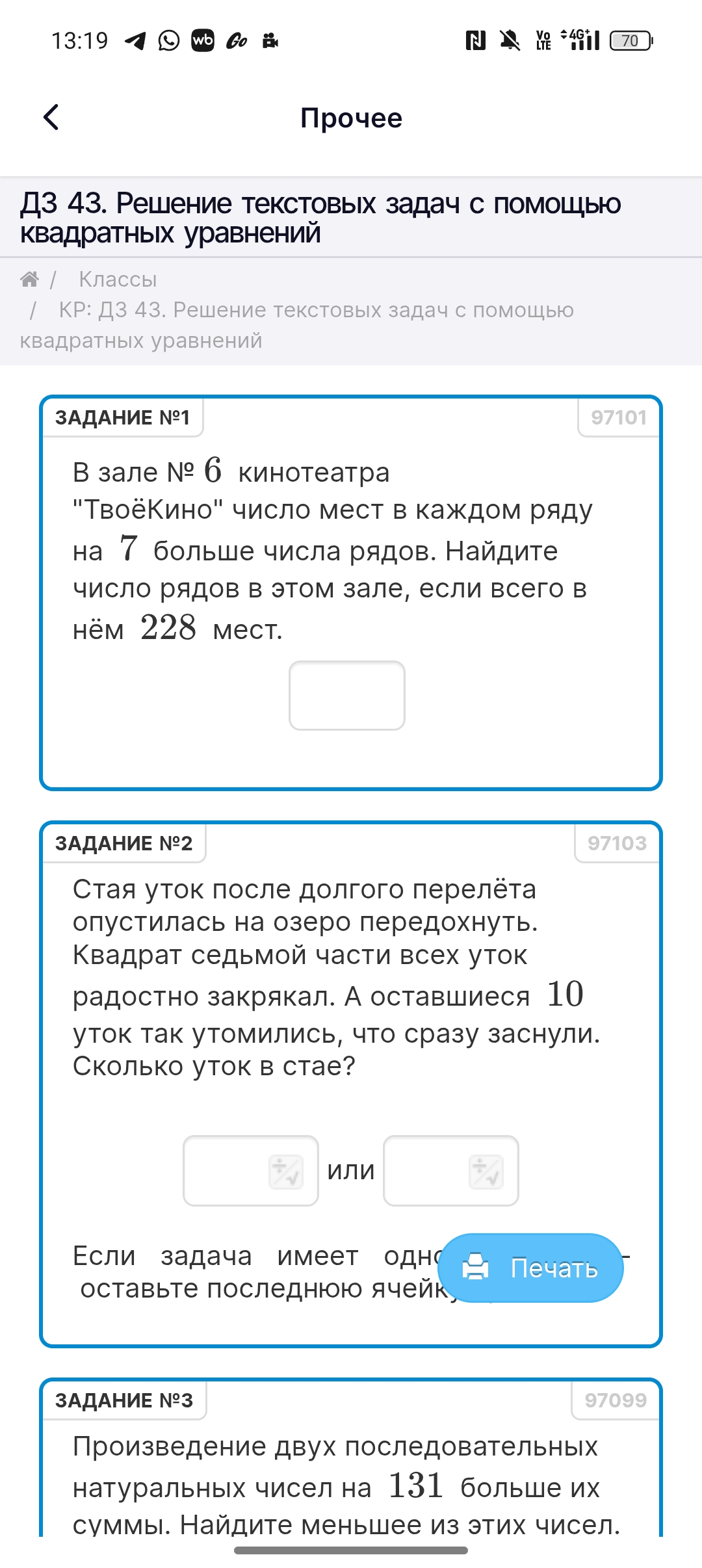
ЗАДАНИЕ №3: Произведение двух последовательных натуральных чисел на 131 больше их суммы. Найдите меньшее из этих чисел.

Пусть меньшее натуральное число равно x. Тогда следующее натуральное число равно x + 1. Произведение этих чисел: x * (x + 1) = x^2 + x. Сумма этих чисел: x + (x + 1) = 2x + 1. По условию задачи, произведение больше суммы на 131: x^2 + x = 2x + 1 + 131 Упростим уравнение: x^2 + x = 2x + 132 Перенесем все слагаемые в левую часть: x^2 + x - 2x - 132 = 0 x^2 - x - 132 = 0 Решим квадратное уравнение. Найдем дискриминант D: D = b^2 - 4ac = (-1)^2 - 4 * 1 * (-132) = 1 + 528 = 529 Найдем корни уравнения: x1 = (-b + sqrt(D)) / 2a = (1 + sqrt(529)) / 2 = (1 + 23) / 2 = 24 / 2 = 12 x2 = (-b - sqrt(D)) / 2a = (1 - sqrt(529)) / 2 = (1 - 23) / 2 = -22 / 2 = -11 Так как число должно быть натуральным, то x = 12. Меньшее из чисел это 12. Проверим (12*13)=156, 12+13=25, 156-25=131. Ответ: 12.