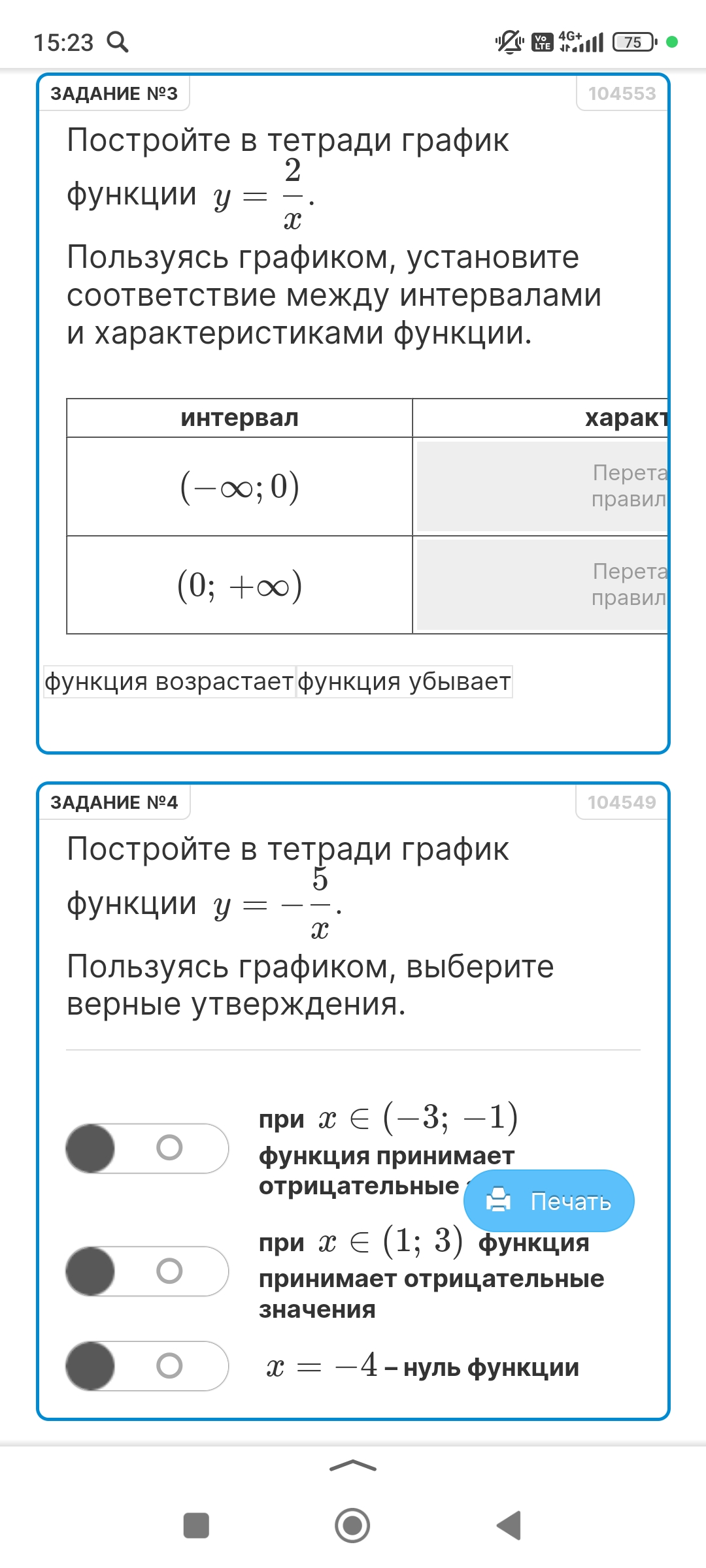
Задание №3. Постройте в тетради график функции \(y = \frac{2}{x}\). Пользуясь графиком, установите соответствие между интервалами и характеристиками функции.

Функция \(y = \frac{2}{x}\) является гиперболой. Рассмотрим ее поведение на разных интервалах: * На интервале \((-\infty; 0)\) функция убывает. При \(x \to -\infty\), \(y \to 0\). При \(x \to 0^-\) (стремится к нулю слева), \(y \to -\infty\). * На интервале \((0; +\infty)\) функция также убывает. При \(x \to 0^+\) (стремится к нулю справа), \(y \to +\infty\). При \(x \to +\infty\), \(y \to 0\). Таким образом, на обоих интервалах функция убывает. | Интервал | Характеристика | |---|---| | \((-\infty; 0)\) | Функция убывает | | \((0; +\infty)\) | Функция убывает |