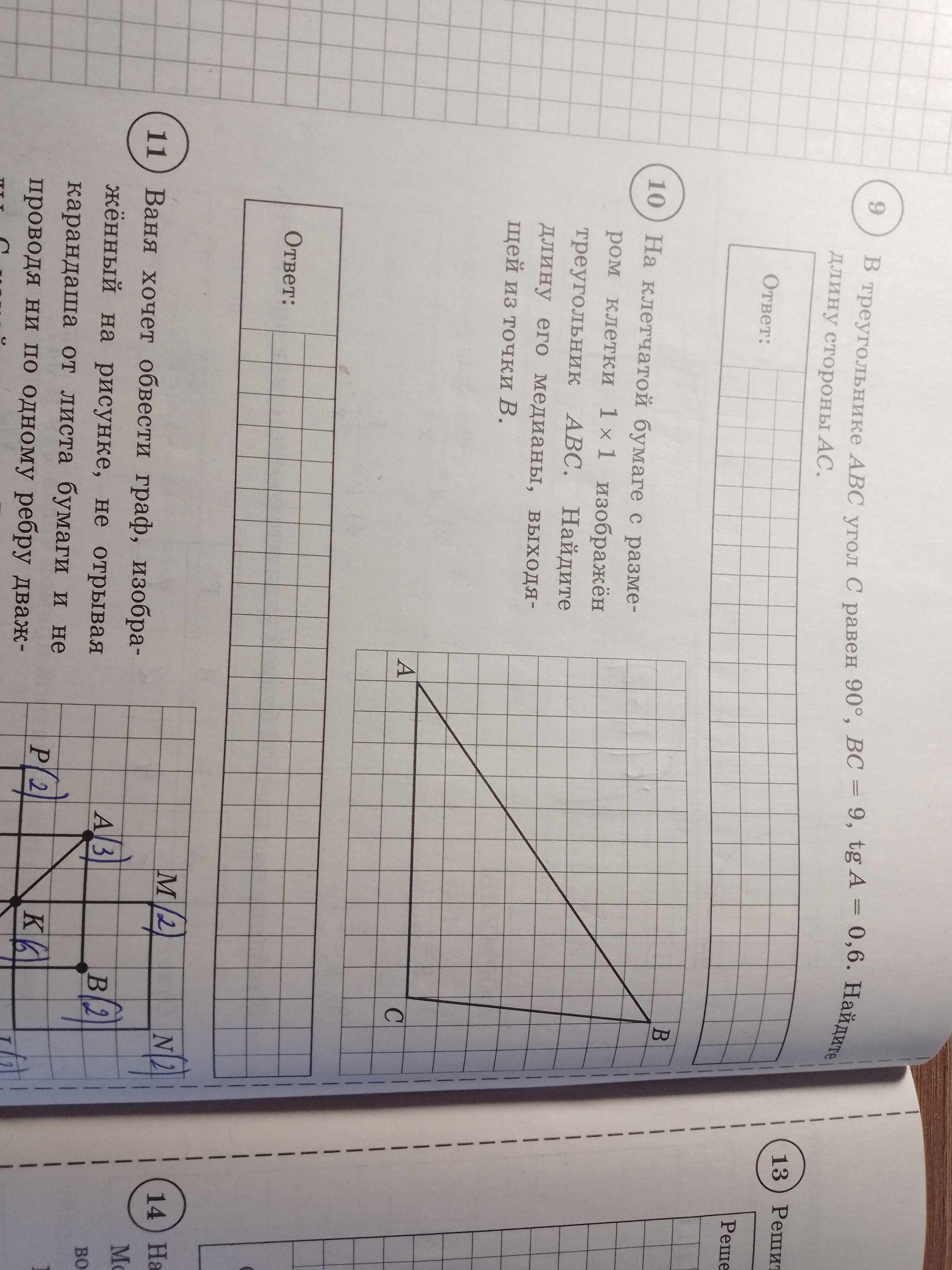
Задание 10: На клетчатой бумаге с размером клетки 1 х 1 изображён треугольник ABC. Найдите длину его медианы, выходящей из точки B.

Решение: Для решения этой задачи нам нужно определить координаты вершин треугольника ABC на клетчатой бумаге. Затем найти середину стороны AC (обозначим её точкой M), и вычислить расстояние между точками B и M (длину медианы). Предположим, что по изображению из условия: * A имеет координаты (0,4) * B имеет координаты (8,0) * C имеет координаты (0,0) 1. Найдем координаты середины стороны AC (точка M): Координаты середины отрезка вычисляются как среднее арифметическое координат концов отрезка. $$M_x = \frac{A_x + C_x}{2} = \frac{0 + 0}{2} = 0$$ $$M_y = \frac{A_y + C_y}{2} = \frac{4 + 0}{2} = 2$$ Таким образом, точка M имеет координаты (0, 2). 2. Найдем расстояние между точками B и M (длину медианы BM): Расстояние между двумя точками на плоскости вычисляется по формуле: $$BM = \sqrt{(B_x - M_x)^2 + (B_y - M_y)^2}$$ $$BM = \sqrt{(8 - 0)^2 + (0 - 2)^2} = \sqrt{8^2 + (-2)^2} = \sqrt{64 + 4} = \sqrt{68}$$ $$BM = \sqrt{4 * 17} = 2\sqrt{17}$$ Приблизительно, $$2\sqrt{17} \approx 8.25$$ Ответ: $$2\sqrt{17}$$, приблизительно 8.25.