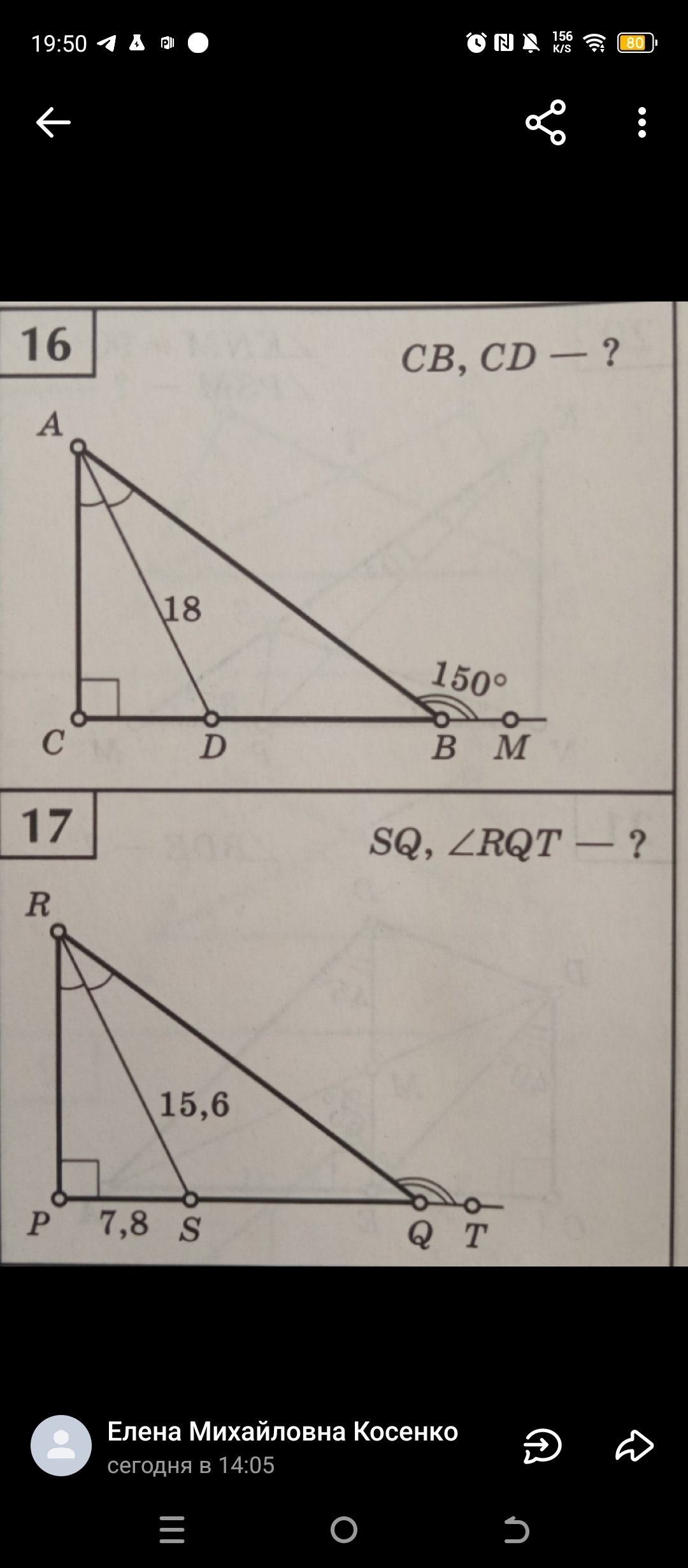
Задача 17: Найти SQ и угол RQT

Задача 17: Дано: Треугольник RPQ, угол P = 90 градусов, RS - биссектриса угла PRQ, PS = 7.8, RQ = 15.6. Найти: SQ и угол RQT. Решение: 1. Рассмотрим треугольник RPQ: RP / RQ = cos(RQT) 2. Найдем RS - биссектрису, делящую угол PRQ пополам. 3. По теореме о биссектрисе треугольника: \(\frac{PS}{SQ} = \frac{RP}{RQ}\), следовательно \(\frac{7.8}{SQ} = \frac{RP}{15.6}\). 4. SQ = PQ - PS = PQ - 7.8. 5. Известно, что RQ = 15.6, PS = 7.8. Рассмотрим прямоугольный треугольник RPS. Выразим RP. По теореме Пифагора, RQ^2 = RP^2 + PQ^2. 6. Заметим, что PS=7.8 и RQ=15.6, значит RQ=2*PS. Пусть угол Q = x. Тогда угол PRQ = 2x. 7. \(sin(2x) = \frac{PQ}{RQ}\) и \(cos(2x) = \frac{RP}{RQ}\). 8. Рассмотрим треугольник RPS: \(RP = \frac{PS}{tan(x)} = \frac{7.8}{tan(x)}\). 9. SQ / PS = RQ / RP => SQ = (PS*RQ)/RP. PQ = SQ + PS. 10. Используем свойство биссектрисы: \(\frac{RP}{RQ} = \frac{PS}{SQ}\). Тогда \(\frac{RP}{15.6} = \frac{7.8}{SQ}\). RP * SQ = 15.6 * 7.8 = 121.68 Пусть PQ = x. Тогда SQ = x - 7.8. По теореме Пифагора: RP^2 + x^2 = 15.6^2 = 243.36. RP^2 = 243.36 - x^2. RP = \(\sqrt{243.36 - x^2}\). SQ = 121.68 / RP = 121.68 / \(\sqrt{243.36 - x^2}\). С другой стороны, SQ = x - 7.8. x - 7.8 = 121.68 / \(\sqrt{243.36 - x^2}\) (x - 7.8) * \(\sqrt{243.36 - x^2}\) = 121.68. Решение этого уравнения достаточно сложно. 11. Найдем угол Q. Поскольку PS = 7.8 и RQ = 15.6, и RS – биссектриса, значит, PS = 1/2 * RQ. Следовательно, угол PRQ = 60 градусов, т.к. тогда sin(30) = PS / RS. Значит угол RQT - внешний для угла RQS, равен 30*2=60. 2x = 60. х=30. sin 60=PQ/RQ. \(\frac{\sqrt{3}}{2}=\frac{PQ}{15.6}\). PQ = 13,5. SQ=13,5-7,8 = 5,7 Ответ: SQ = 5.7, угол RQT = 30 градусов (внешний -60 градусов)