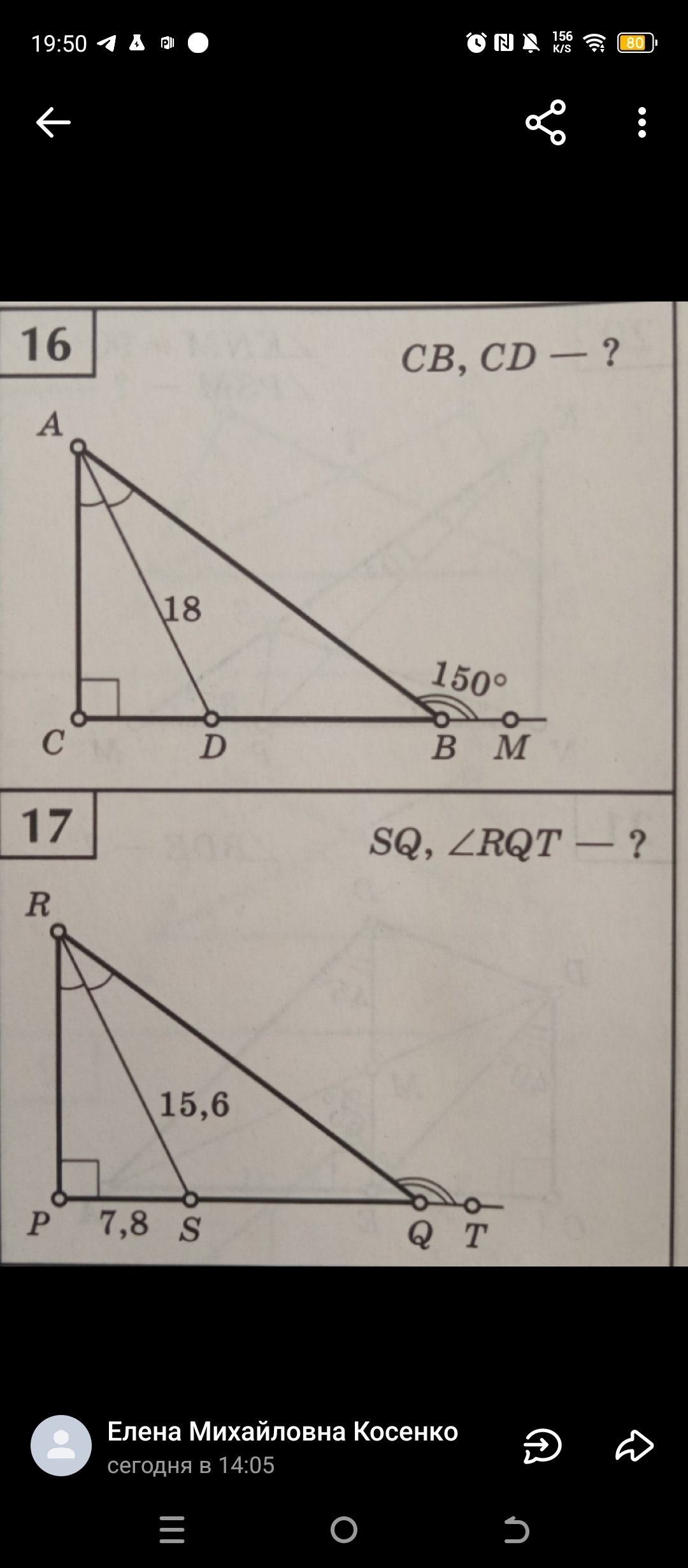
Задача 16: Найти CB и CD

Задача 16: Дано: Треугольник ABC, угол C = 90 градусов, AD - биссектриса угла BAC, угол ABM = 150 градусов, AD = 18. Найти: CB и CD. Решение: 1. Угол ABC = 180 - 150 = 30 градусов (смежные углы). 2. В прямоугольном треугольнике ABC, угол BAC = 180 - 90 - 30 = 60 градусов. 3. Так как AD - биссектриса угла BAC, то угол CAD = угол BAD = 60 / 2 = 30 градусов. 4. Рассмотрим треугольник ADC: угол CAD = 30 градусов, угол ACD = 90 градусов, значит угол ADC = 180 - 90 - 30 = 60 градусов. 5. В треугольнике ADC: AD = 18 (дано). 6. CD / AD = sin(CAD) = sin(30) = 1/2. Следовательно, CD = AD * (1/2) = 18 * (1/2) = 9. 7. AC / AD = cos(CAD) = cos(30) = \(\frac{\sqrt{3}}{2}\). Следовательно, AC = AD * \(\frac{\sqrt{3}}{2}\) = 18 * \(\frac{\sqrt{3}}{2}\) = 9\(\sqrt{3}\). 8. Рассмотрим треугольник ABC: AC = 9\(\sqrt{3}\), угол ABC = 30 градусов. 9. AC / CB = tan(ABC) = tan(30) = \(\frac{1}{\sqrt{3}}\) = \(\frac{\sqrt{3}}{3}\). 10. Следовательно, CB = AC / tan(30) = 9\(\sqrt{3}\) / \(\frac{\sqrt{3}}{3}\) = 9\(\sqrt{3}\) * \(\frac{3}{\sqrt{3}}\) = 27. Ответ: CB = 27, CD = 9.