В геометрической прогрессии {a_n} с положительными членами a_2=8; a_4=72. Найдите сумму первых пяти членов этой прогрессии.

\[a_{2} = 8 \Longrightarrow a_{2} = b_{1} \cdot q;\ \ \ \]

\[a_{4} = 72 \Longrightarrow a_{4} = b_{1} \cdot q^{3}\]

\[\frac{b_{1}q^{3}}{b_{1}q} = \frac{72}{8} = 9 \Longrightarrow q^{2} = 9 \Longrightarrow\]

\[\Longrightarrow q = 3;\ \ так\ как\ \left\{ a_{n} \right\} > 0\]

\[8 = b_{1} \cdot 3 \Longrightarrow b_{1} = 2\frac{2}{3}\]

\[S_{5} = \frac{b_{1} \cdot \left( 1 - q^{5} \right)}{1 - q} =\]

\[= \frac{\frac{8}{3} \cdot \left( 1 - 3^{5} \right)}{1 - 3} = \frac{\frac{8}{3} \cdot (1 - 243)}{- 2} =\]

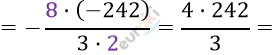
\[= \frac{968}{3} = 322\frac{2}{3}\]

\[Ответ:\ \ 322\frac{2}{3}.\]