Сумма квадратов цифр двузначного числа равна 45. Если из этого числа вычесть 27, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.

\[Пусть\ x - цифра\ единиц\ \]

\[двузначного\ числа,\ тогда\ \]

\[y - цифра\ десятков\ этого\ же\ \]

\[числа.\ \]

\[Составим\ и\ решим\ систему\ \]

\[уравнений:\]

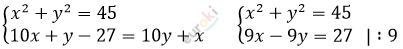
\[\left\{ \begin{matrix} x^{2} + y^{2} = 45\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x - y = 3 \Longrightarrow x = 3 + y \\ \end{matrix} \right.\ \]

\[(3 + y)^{2} + y^{2} = 45\]

\[9 + 6y + y^{2} + y^{2} = 45\]

\[2y^{2} + 6y - 36 = 0\ \ \ \ \ \ \ |\ :2\]

\[y^{2} + 3y - 18 = 0\]

\[D = 9 + 18 \cdot 4 = 81\]

\[y_{1} = \frac{- 3 + 9}{2} = 3;\ \ \ \ \]

\[\text{\ \ }y_{2} = \frac{- 3 - 9}{2} = - 6\]

\[x_{1} = 3 + 3 = 6;\ \ \ \ \ \ \ \]

\[\text{\ \ \ }x_{2} = - 6 + 3 = - 3.\]

\[Отрицательные\ значения\ \]

\[не\ подходят,\ значит\ искомое\ \]

\[число\ 63.\]

\[Ответ:\ \ 63.\]