Решите задачу №8. Найдите угол \(\angle ABC\).

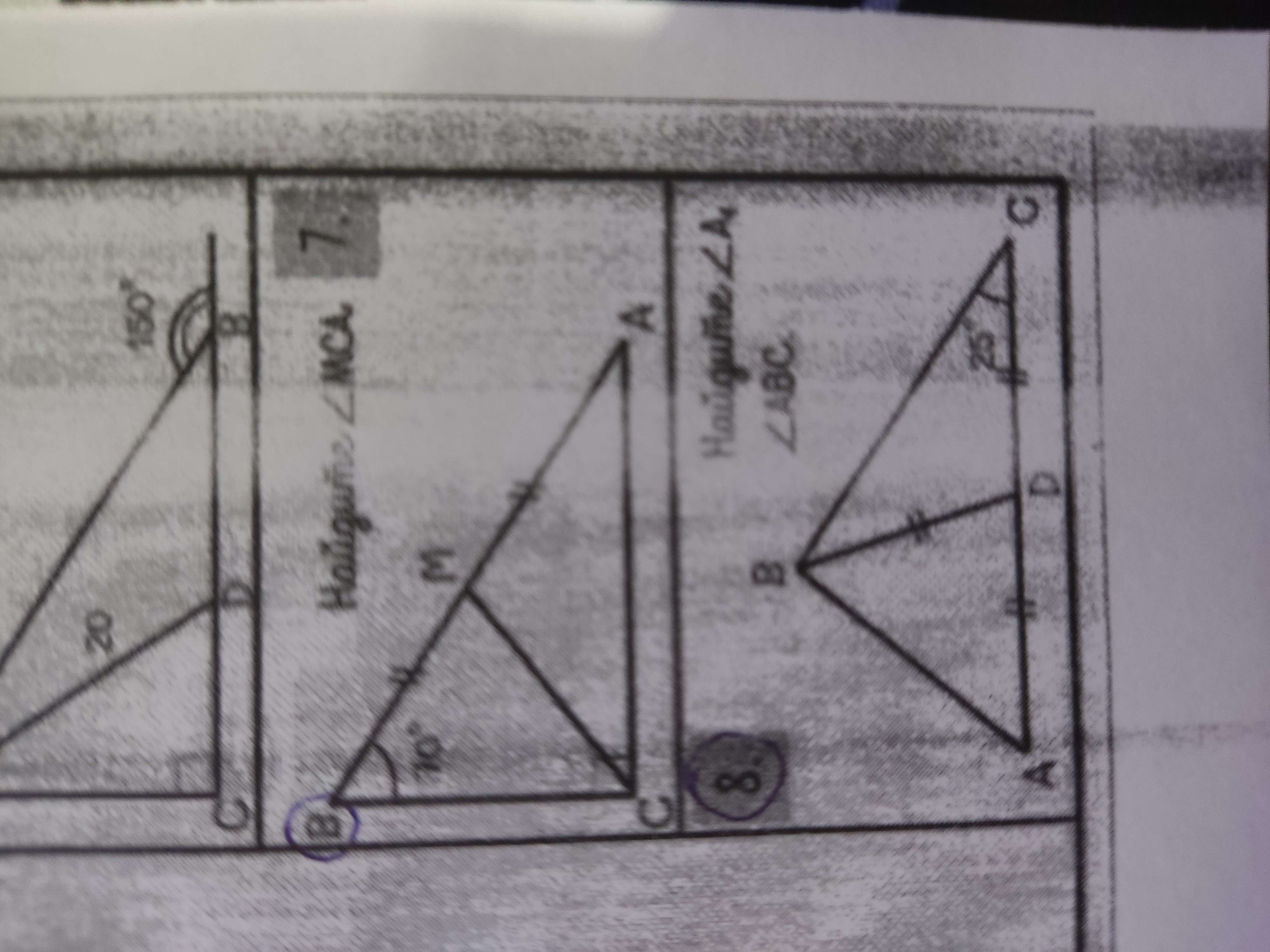
Давайте решим задачу №8. Нам дан треугольник \(\triangle ABC\), в котором \(AB = BC\), а \(\angle MBC = 10^{\circ}\). Также известно, что \(AM = MC\). Нужно найти угол \(\angle ABC\). 1. Определение типов треугольников: * Поскольку \(AB = BC\), треугольник \(\triangle ABC\) является равнобедренным. В равнобедренном треугольнике углы при основании равны, то есть \(\angle BAC = \angle BCA\). * Так как \(AM = MC\), то треугольник \(\triangle AMC\) является равнобедренным, а значит, \(\angle MAC = \angle MCA\). 2. Обозначение углов: * Пусть \(\angle MAC = \angle MCA = x\). Тогда \(\angle BAC = \angle BCA = x\) (так как \(\triangle ABC\) равнобедренный). 3. Выражение угла \(\angle ABC\) через \(x\): * Сумма углов в треугольнике \(\triangle ABC\) равна 180 градусов. Следовательно: \(\angle ABC + \angle BAC + \angle BCA = 180^{\circ}\) \(\angle ABC + x + x = 180^{\circ}\) \(\angle ABC = 180^{\circ} - 2x\) 4. Использование информации о \(\angle MBC\): * Мы знаем, что \(\angle BCA = x\), и \(\angle MBC = 10^{\circ}\). * Тогда \(\angle MBA = \angle ABC - \angle MBC\). 5. Анализ треугольника \(\triangle ABM\). *Рассмотрим \(\triangle ABC\), т.к \(AM=MC\) и \(\angle MAC = \angle MCA = x\), а \(\angle MBC = 10^{\circ}\), и \(\angle BAC = \angle BCA = x\), то \(BM\) - биссектриса. Тогда \(\angle MBA = \angle MBC = 10^{\circ}\) 6. Подставляем значения и находим \(\angle ABC\): \(\angle ABC = \angle MBA+\angle MBC\) \(\angle ABC = 10^{\circ}+10^{\circ}=20^{\circ}\) * Ответ: \(\angle ABC = 20^{\circ}\)