Решите уравнение: (x^2+20)/(x^2-4)=(x-3)/(x+2)-6/(2-x).

\[\frac{x^{2} + 20}{x^{2} - 4} = \frac{x - 3^{\backslash x\text{-}2}}{x + 2} - \frac{6^{\backslash x + 2}}{2 - x}\]

\[\frac{x^{2} + 20}{(x - 2)(x + 2)} =\]

\[= \frac{(x - 3)(x - 2) + 6 \cdot (x + 2)}{(x - 2)(x + 2)};\ \ \]

\[x \neq 2,\ x \neq - 2\]

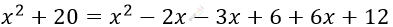
\[20 + 2x + 3x - 6 - 6x - 12 = 0\]

\[- x + 2 = 0\]

\[x = 2\ (не\ подходит).\]

\[Ответ:нет\ решения.\]