Решите уравнение: корень 4 степени из (x^4+4x^3+8,5)=x+1.

\[\sqrt[4]{x^{4} + 4x^{3} + 8,5} = x + 1\]

\[x^{4} + 4x^{3} + + 8,5 = (x + 1)^{4}\]

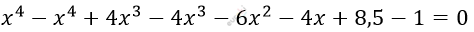
\[- 6x^{2} - 4x + 7,5 = 0\ \ \ \ | \cdot ( - 2)\]

\[12x^{2} + 8x - 15 = 0\]

\[D = 16 + 180 = 196\]

\[x_{1} = \frac{- 4 + 14}{12} = \frac{10}{12} = \frac{5}{6};\ \ \ \]

\[x_{2} = \frac{- 4 - 14}{12} = - \frac{18}{12} =\]

\[= - \frac{3}{2} = - 1,5\]

\[Проверка.\]

\[x = \frac{5}{6}:\]

\[\sqrt[4]{\frac{625}{1296} + 4 \cdot \frac{125}{216} + \frac{17}{2}} =\]

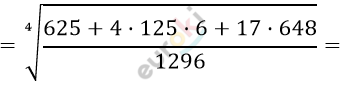
\[= \sqrt[4]{\frac{625 + 3000 + 11\ 016}{1296}} =\]

\[= \sqrt[4]{\frac{14641}{1296}} = \frac{11}{6};\]

\[\frac{5}{6} + 1 = \frac{5 + 6}{6} = \frac{11}{6}.\]

\[x = \frac{5}{6} - корень\ уравнения.\]

\[x = - \frac{3}{2}:\]

\[\sqrt[4]{\frac{81}{16} + 4 \cdot \left( - \frac{27}{8} \right) + \frac{17}{2}} =\]

\[= \sqrt[4]{\frac{81 - 216 + 136}{16}} =\]

\[= \sqrt[4]{\frac{1}{16}} = \frac{1}{2};\]

\[x + 1 = - \frac{3}{2} + 2 = - \frac{1}{2};\]

\[\frac{1}{2} \neq - \frac{1}{2}\]

\[x = - \frac{3}{2} - не\ является\ корнем\ \]

\[уравнения.\]

\[Ответ:x = \frac{5}{6}.\]