Решите уравнение: 3x^3+13x^2+13x+3=0.

\[3x^{3} + 13x^{2} + 13x + 3 = 0\]

\[3 \bullet \left( x^{3} + 1 \right) + 13x(x + 1) = 0\]

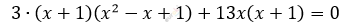
\[(x + 1)\left( 3x^{2} - 3x + 3 + 13x \right) =\]

\[= 0\]

\[(x + 1)\left( 3x^{2} + 10x + 3 \right) = 0\]

\[x + 1 = 0 \Longrightarrow x = - 1.\]

\[3x^{2} + 10x + 3 = 0\]

\[D = 10^{2} - 4 \cdot 3 \cdot 3 = 100 - 36 =\]

\[= 64\]

\[x_{1} = \frac{- 10 + \sqrt{64}}{2 \cdot 3} = \frac{- 10 + 8}{6} =\]

\[= \frac{- 2}{6} = - \frac{1}{3}\]

\[x_{2} = \frac{- 1 - \sqrt{64}}{2 \cdot 3} = \frac{- 10 - 8}{6} =\]

\[= \frac{- 18}{6} = - 3\]

\[Ответ:\ x = - 1;x = \ - \frac{1}{3};\ \]

\[x = - 3.\]