Решите систему уравнений: x+2y/(x-y)-3x-3y/(x+2y)=2; x-2y=-5.

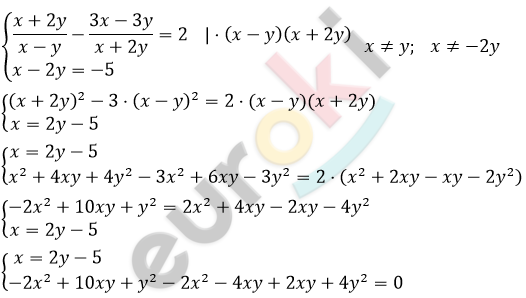
\[\left\{ \begin{matrix} x = 2y - 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ - 4x^{2} + 8xy + 5y^{2} = 0 \\ \end{matrix} \right.\ \]

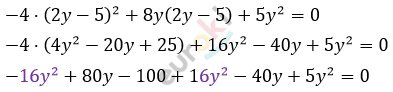
\[5y^{2} + 40y - 100 = 0\ \ \ \ \ \ \ |\ :5\]

\[y^{2} + 8y - 20 = 0\]

\[D = 8^{2} - 4 \cdot 1 \cdot ( - 20) =\]

\[= 64 + 80 = 144;\ \ \ \ \sqrt{D} = 12.\]

\[y_{1} = \frac{- 8 + 12}{2} = \frac{4}{2} = 2;\ \ \ \ \ \]

\[y_{2} = \frac{- 8 - 12}{2} = \frac{- 20}{2} = - 10\]

\[x_{1} = 2 \cdot 2 - 5 = - 1;\ \ \ \ \ \]

\[\text{\ \ \ \ }x_{2} = 2 \cdot ( - 10) - 5 =\]

\[= - 20 - 5 = - 25\]

\[Ответ:( - 1;2);\ \ ( - 25;\ - 10).\]