Решите неравенство: x^4+x^3<=(x+1)/x.

\[x^{4} + {x^{3}}^{\backslash x} \leq \frac{x + 1}{x}\]

\[\frac{\left( x^{4} + x^{3} \right)x - (x + 1)}{x} \leq 0\]

\[\frac{x^{4}(x + 1) - (x + 1)}{x} \leq 0\]

\[\frac{(x + 1)(x^{4} - 1)}{x} \leq 0\]

\[\frac{(x + 1)\left( x^{2} - 1 \right)\left( x^{2} + 1 \right)}{x} \leq 0\]

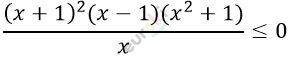
\[\frac{(x + 1)^{2}(x - 1)}{x} \leq 0\]

\[Ответ:\left\{ - 1 \right\} \cup (0;1\rbrack.\]