Решите неравенство: 10x/(x+6)-4*корень из (10x/(x+6))-5>=0.

\[\frac{10x}{x + 6} - 4\sqrt{\frac{10x}{x + 6}} - 5 \geq 0\]

\[t = \sqrt{\frac{10x}{x + 6}}\]

\[t^{2} - 4t - 5 \geq 0\]

\[(t - 5)(t + 1) \geq 0\]

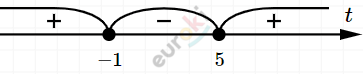
\[t \leq - 1;\ \ \ t \geq 5.\]

\[1)\ \sqrt{\frac{10x}{x + 6}} \leq - 1\]

\[\sqrt{\frac{10x}{x + 6}} \geq 0 \Longrightarrow нет\ решения.\]

\[2)\ \sqrt{\frac{10x}{x + 6}} \geq 5\ \]

\[\frac{10x}{x + 6} \geq 25\]

\[\frac{10x - 25 \cdot (x + 6)}{x + 6} \geq 0\]

\[\frac{10x - 25x - 150}{x + 6} \geq 0\]

\[\frac{- 15x - 150}{x + 6} \geq 0\]

\[\frac{- 15 \cdot (x + 10)}{x + 6} \geq 0\]

\[\frac{x + 10}{x + 6} \leq 0\]

\[Ответ:\lbrack - 10; - 6).\]