При любом n сумму n первых членов некоторой арифметической прогрессии можно вычислить по формуле Sn=5n^2-3n. Найдите первый член и разность этой прогрессии.

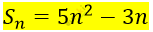
\[S_{2} = 5 \cdot 4 - 6 = 14\ \]

\[S_{4} = 5 \cdot 16 - 12 = 68\]

\[\left\{ \begin{matrix} \frac{2a_{1} + d}{2} \cdot 2 = 14\ \ \\ \frac{2a_{1} + 3d}{2} \cdot 4 = 68 \\ \end{matrix}\text{\ \ \ \ \ \ \ \ } \right.\ \]

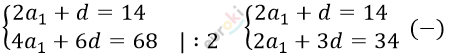
\[\left\{ \begin{matrix} - 2a = - 20\ \ \ \\ a_{1} = \frac{14 - d}{2}\text{\ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} d = 10 \\ a_{1} = 2 \\ \end{matrix} \right.\ \]

\[Ответ:a_{1} = 2;\ \ \ \ \ d = 10.\]