При каких значениях параметра a уравнение ax²+(a²+1)x+a=0: имеет единственный корень.

\[ax + \left( a^{2} + 1 \right)x + a = 0\]

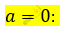
\[0 \cdot x^{2} + \left( 0^{2} + 1 \right)x + 0 = 0\]

\[x = 0.\]

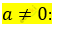
\[D = \left( a^{2} + 1 \right)^{2} - 4 \cdot a \cdot a = 0\]

\[a^{4} + 2a^{2} + 1 - 4a^{2} = 0\]

\[a^{4} - 2a^{2} + 1 = 0\]

\[\left( a^{2} - 1 \right)^{2} = 0\]

\[a^{2} - 1 = 0\]

\[a = \pm 1.\]

\[Ответ:\ при\ a = 0;\ \ \ a = \pm 1\]