При каких значениях параметра a числа 4 и 6 являются решениями системы неравенств x-2a<3; 2x-a>3?

\[\left\{ \begin{matrix}
x - 2a < 3 \\
2x - a > 3 \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix}
x < 2a + 3 \\
2x > a + 3 \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix}
x < 2a + 3 \\
x > \frac{a + 3}{2}\ \\
\end{matrix} \right.\ \]

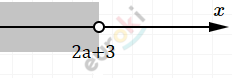\(\text{\ \ \ \ \ \ \ \ \ \ }\)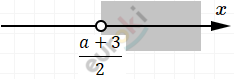

\[Числа\ 4\ и\ 6\ решения\ при:\]

\[\frac{a + 3}{2} < 4 < 6 < 2a + 3\]

\[\left\{ \begin{matrix}
2a + 3 > 6 \\
\frac{a + 3}{2} < 4\ \ \ \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix}
2a > 3\ \ \ \ \ \ \\
a + 3 < 8 \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix}
a > 1,5 \\
a < 5\ \ \ \\
\end{matrix} \right.\ \]

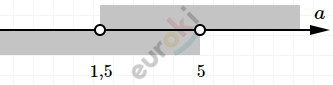
\[Ответ:при\ a \in (1,5;5).\]