Вопрос:
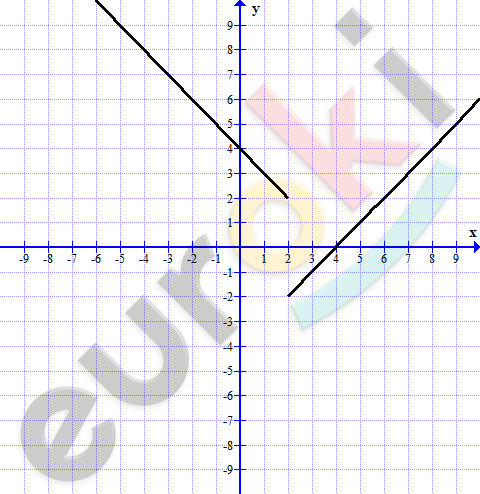
Постройте график функции: y=(x^2-6x+8)/корень из (x^2-4x+4).
Ответ:
\[y = \frac{x^{2} - 6x + 8}{\sqrt{x^{2} - 4x + 4}} =\]
\[= \frac{(x - 4)(x - 2)}{\sqrt{(x - 2)^{2}}} =\]
\[= \frac{(x - 4)(x - 2)}{|x - 2|};\ \ \ \ \ x
eq 2\]
\[x^{2} - 6x + 8 = 0\]
\[D = ( - 6)^{2} - 4 \cdot 1 \cdot 8 =\]
\[= 36 - 32 = 4;\ \ \ \sqrt{D} = 2.\]
\[x_{1} = \frac{6 + 2}{2} = \frac{8}{2} = 4;\ \ \]
\[\ x_{2} = \frac{6 - 2}{2} = \frac{4}{2} = 2.\]
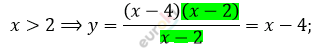
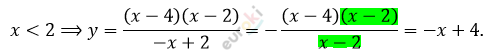
Похожие
- Бригада трактористов должна была вспахать 168 га к определенному сроку. Но ежедневно бригада вспахивала на 2 га больше, чем намечено по плану, поэтому за 1 день до срока она перевыполнила задание на 14 га. Сколько гектаров в день вспахивала бригада?
- Постройте график функции: y=-1/2 x+3. С помощью определения докажите, что функция y=-1/2 x+3 является возрастающей на множестве R.
- Постройте график функции: y=|-1/2 x+3|. С помощью определения докажите, что функция y=-1/2 x+3 является возрастающей на множестве R.