Постройте график функции f(x)=x^2+2x-3. Используя этот график, найдите: множество решений неравенства f(x)>=0; f(x)<0.

\[f(x) = x^{2} + 2x - 3\]

\[x_{0} = \frac{- 2}{2} = - 1;\text{\ y}_{0} = - 4\]

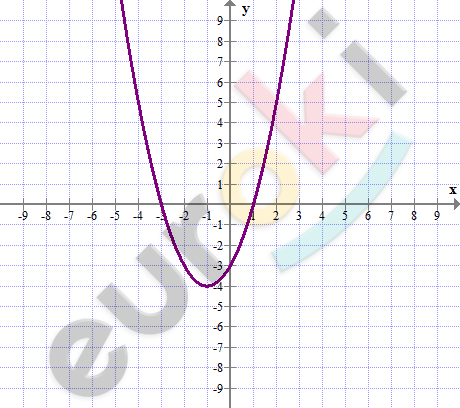
\[f(x) \geq 0\ \ \ при\ \ \ \ x \leq - 3\ \ \ \]

\[и\ \ x \geq 1;\]

\[f(x) < 0\ \ \ \ при\ \ \ - 3 < x < 1.\]