Первый экскаватор работал на рытье котлована 2 ч, после чего к нему присоединился второй экскаватор. Через 1 ч совместной работы была вырыта 1/4 котлована. За сколько часов может вырыть котлован каждый экскаватор самостоятельно, если второму для этого требуется на 6 ч меньше, чем первому?

Ответ:

\[Пусть\ x\ часов - надо\ первому\ \]

\[экскаватору,\ \]

\[(x - 6)\ часов - надо\ второму\ \]

\[экскаватору.\]

\[1 - весь\ котлован.\]

\[Вместе\ они\ вырыли\ \frac{1}{4}\ \ часть\ \]

\[котлована.\]

\[Составим\ уравнение:\ \]

\[2 \cdot \frac{1}{x} + \left( \frac{1}{x} + \frac{1}{x - 6} \right) = \frac{1}{4}\]

\[\frac{2}{x} + \frac{1}{x} + \frac{1}{x - 6} - \frac{1}{4} = 0\]

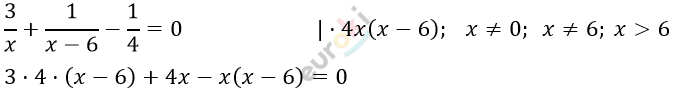
\[12x - 72 + 4x - x^{2} + 6x = 0\]

\[- x^{2} + 22x - 72 = 0\]

\[x^{2} - 22x + 72 = 0\]

\[x_{1} + x_{2} = 22;\ \ x_{1} \cdot x_{2} = 72\]

\[x_{1} = 18\ (ч) - надо\ первому\ \]

\[экскаватору.\]

\[x_{2} = 4\ (не\ подходит).\]

\[x - 6 = 18 - 6 = 12\ (ч) - надо\ \]

\[второму\ экскаватору.\]

\[Ответ:18\ часов;\ \ 12\ часов.\]