Освободитесь от иррациональности в знаменателе дроби: 1/(2 корня из 2+2 корня из 3-корень из 6-2).

\[\frac{1}{2\sqrt{2} + 2\sqrt{3} - \sqrt{6} - 2} =\]

\[= \frac{1}{2 \cdot \left( \sqrt{2} + \sqrt{3} \right) - \sqrt{2}\left( \sqrt{2} + \sqrt{3} \right)} =\]

\[= \frac{1}{\left( 2 - \sqrt{2} \right)\left( \sqrt{2} + \sqrt{3} \right)} =\]

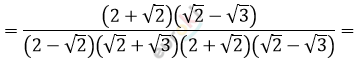
\[= \frac{\left( 2 + \sqrt{2} \right)\left( \sqrt{2} - \sqrt{3} \right)}{(4 - 2)(2 - 3)} =\]

\[= \frac{\left( 2 + \sqrt{2} \right)\left( \sqrt{2} - \sqrt{3} \right)}{2 \cdot ( - 1)} =\]

\[= \frac{\left( 2 + \sqrt{2} \right)\left( \sqrt{3} - \sqrt{2} \right)}{2}\]