Определите номер наименьшего члена последовательности, заданной формулой n-го члена c_n=n^2-23 1/3 n+21.

\[c_{n} = n^{2} - 23\frac{1}{3}n + 21 =\]

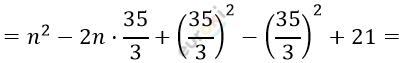
\[= \left( n - \frac{35}{3} \right)^{2} - \left( 36\frac{1}{9} + 2 \right) =\]

\[= \left( n - 11\frac{2}{3} \right)^{2} - 115\frac{1}{9} \Longrightarrow\]

\[\Longrightarrow n = 11\ или\ 12.\]

\[c_{11} = \left( 11 - 11\frac{2}{3} \right)^{2} - 115\frac{1}{9} =\]

\[= \left( - \frac{2}{3} \right)^{2} - 115\frac{1}{9} = \frac{4}{9} - 115\frac{1}{9} =\]

\[= - 114\frac{2}{3}\]

\[c_{12} = \left( 12 - 11\frac{2}{3} \right)^{2} - 115\frac{1}{9} =\]

\[= \left( \frac{1}{3} \right)^{2} - 115\frac{1}{9} = \frac{1}{9} - 115\frac{1}{9} =\]

\[= - 115\]

\[- 115 < - 114\frac{2}{3} \Longrightarrow\]

\[\Longrightarrow c_{12} - наименьший.\]

\[Ответ:12.\]