Одновременно из одного села в одном направлении выехали два велосипедиста: первый со скоростью 12 км/ч, а второй – 15 км/ч. Через 4 ч из этого села в том же направлении выехал автомобиль. Найдите скорость автомобиля, если известно, что он догнал второго велосипедиста через 20 мин после того, как догнал первого.

Ответ:

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[легкового\ автомобиля;\]

\[t\ часов - время\ встречи.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} (t + 1) \cdot 40 = tx\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ t + 1 = \frac{300 - (t + 1) \cdot 40}{x} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} (t + 1) \cdot 40 = tx\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ t + 1 = \frac{300 - 40t - 40}{x} \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} (t + 1) \cdot 40 = tx\ \ \ \\ t + 1 = \frac{260 - 40t}{x} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} (t + 1) \cdot 40 = tx \\ x = \frac{260 - 40t}{t + 1}\text{\ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} (t + 1) \cdot 40 = \frac{t(260 - 40t)}{t + 1} \\ x = \frac{260 - 40t}{t + 1}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]

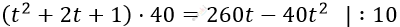
\[4t^{2} + 8t + 4 - 26t + 4t^{2} = 0\]

\[8t² - 18t + 4 = 0\ \ \ |\ :2\]

\[4t^{2} - 9t + 2 = 0\]

\[D = 81 - 32 = 49\]

\[t_{1} = \frac{9 - 7}{8} = \frac{1}{4}\ (ч) - время\ \]

\[встречи.\ \ \]

\[t_{2} = \frac{9 + 7}{8} = 2\ (ч) - время\ \]

\[встречи.\]

\[\frac{260 - 40 \cdot \frac{1}{4}}{\frac{1}{4} + 1} = 250 \cdot \frac{4}{5} =\]

\[= 200 - не\ может\ быть.\]

\[\frac{260 - 40 \cdot 2}{2 + 1} = \frac{180}{3} =\]

\[= 60\ \left( \frac{км}{ч} \right) - скорость\ \]

\[первого\ автомобиля.\]

\[Ответ:60\frac{км}{ч}.\]