Чтобы переместить груз из точки A в точку B, его сначала поднимают по наклонной поверхности, а затем опускают также по наклонной поверхности, причём подъём происходит со скоростью на 2 м/с большей, чем спуск. Длина пути, который проходит груз из точки A в точку B, равна 120 м, и длится это перемещение 14 с. Если бы груз перемещали из точки B в точку A, то перемещение длилось бы 13 с. Найдите скорость подъема и скорость спуска груза.

\[Пусть\ x\frac{км}{ч} - скорость\ \]

\[автомобиля,\ t - время,\ \]

\[за\ которое\ он\ догнал\]

\[первого\ велосипедиста.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} tx = (t + 4) \cdot 12\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \left( t + \frac{20}{60} \right)x = \left( t + 4 + \frac{20}{60} \right) \cdot 15 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} tx = 12t + 48\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ tx + \frac{1}{3}x = 15t + \frac{13 \cdot 15}{3} \\ \end{matrix} \right.\ \]

\[x = \frac{12t + 48}{t}\]

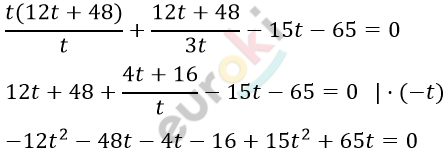
\[3t^{2} + 13t - 16 = 0\]

\[D = 169 + 192 = 361\]

\[t = \frac{- 13 + 19}{6} = 1\ (ч) - догнал\ \]

\[первого\ велосипедиста.\ \ \]

\[t = \frac{- 13 - 19}{6} < 0.\]

\[12 \cdot 1 + 48 = 60\ \left( \frac{км}{ч} \right) -\]

\[скорость\ автомобиля.\]

\[Ответ:60\ \frac{км}{ч}.\]