Одновременно из одного города в одном направлении выехали два мотоциклиста: первый со скоростью 80 км/ч, а второй – 60 км/ч. Через полчаса из этого города в том же направлении выехал третий мотоциклист. Найдите скорость третьего мотоциклиста, если известно, что он догнал первого мотоциклиста через 1 ч 15 мин после того, как догнал второго.

Ответ:

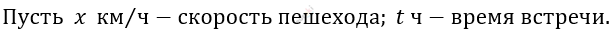
\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} 15t = (t + 2)\text{x\ \ \ \ \ \ \ \ } \\ tx = 20 - (t + 2)x \\ \end{matrix}\text{\ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} 15t = tx + 2x \\ tx = 20 - 15t \\ \end{matrix} \right.\ \]

\[tx = 20 - tx - 2x\]

\[2tx = 20 - 2x\ \ \ \ \ \ |\ :2\ \ \ \]

\[tx = 10 - x\]

\[tx + x = 10\ \ \]

\[\text{\ x}(t + 1) = 10\]

\[x = \frac{10}{t + 1}\]

\[15t = \frac{10t}{t + 1} + \frac{20}{t + 1}\]

\[15t(t + 1) = 10 \cdot (t + 2)\]

\[15t^{2} + 15t - 10t - 20 = 0\ \ \ \]

\[15t^{2} + 5t - 20 = 0\ \ \ \ \ |\ :5\]

\[3t^{2} + t - 4 = 0\ \ \]

\[D = 1 + 48 = 49,\ \]

\[t = \frac{- 1 + 7}{6} = 1\ \]

\[t = \frac{- 1 - 7}{6} - не\ удовлетворяет.\]

\[t = 1.\ \ \ \]

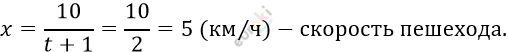
\[Ответ:5\ \frac{км}{ч.}\]