Вопрос:
Найдите значение рационального выражения: x^2/(x^2+2x+1)-(3x-4)/(3x+3) при x=19.
Ответ:
\[\frac{x^{2}}{x^{2} + 2x + 1} - \frac{3x - 4}{3x + 3} =\]
\[= \frac{x^{2}}{(x + 1)^{2}} - \frac{3x - 4}{3 \cdot (x + 1)} =\]
\[= \frac{3x^{2} - (3x - 4)(x + 1)}{3 \cdot (x + 1)^{2}} =\]
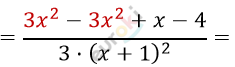
\[= \frac{x - 4}{3 \cdot (x + 1)^{2}} = \frac{19 - 4}{3 \cdot (19 + 1)^{2}} =\]
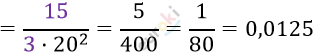
Похожие
- Найдите значение рационального выражения: (2x+24)/(x^2-9)+3/(x+3) при x=1997.
- Найдите значение рационального выражения: (8a^3-b^3)/(4a^2+2ab+b^2)+(8a^3+b^3)/(4a^2-2ab+b^2) при a=0,05, b=-13 14/15.
- Преобразуйте в алгебраическую дробь рациональное выражение 2/(x+3)+18x/(x^3+27)-(x+3)/(x^2-3x+9) и найдите значение полученной дроби при x=-3.