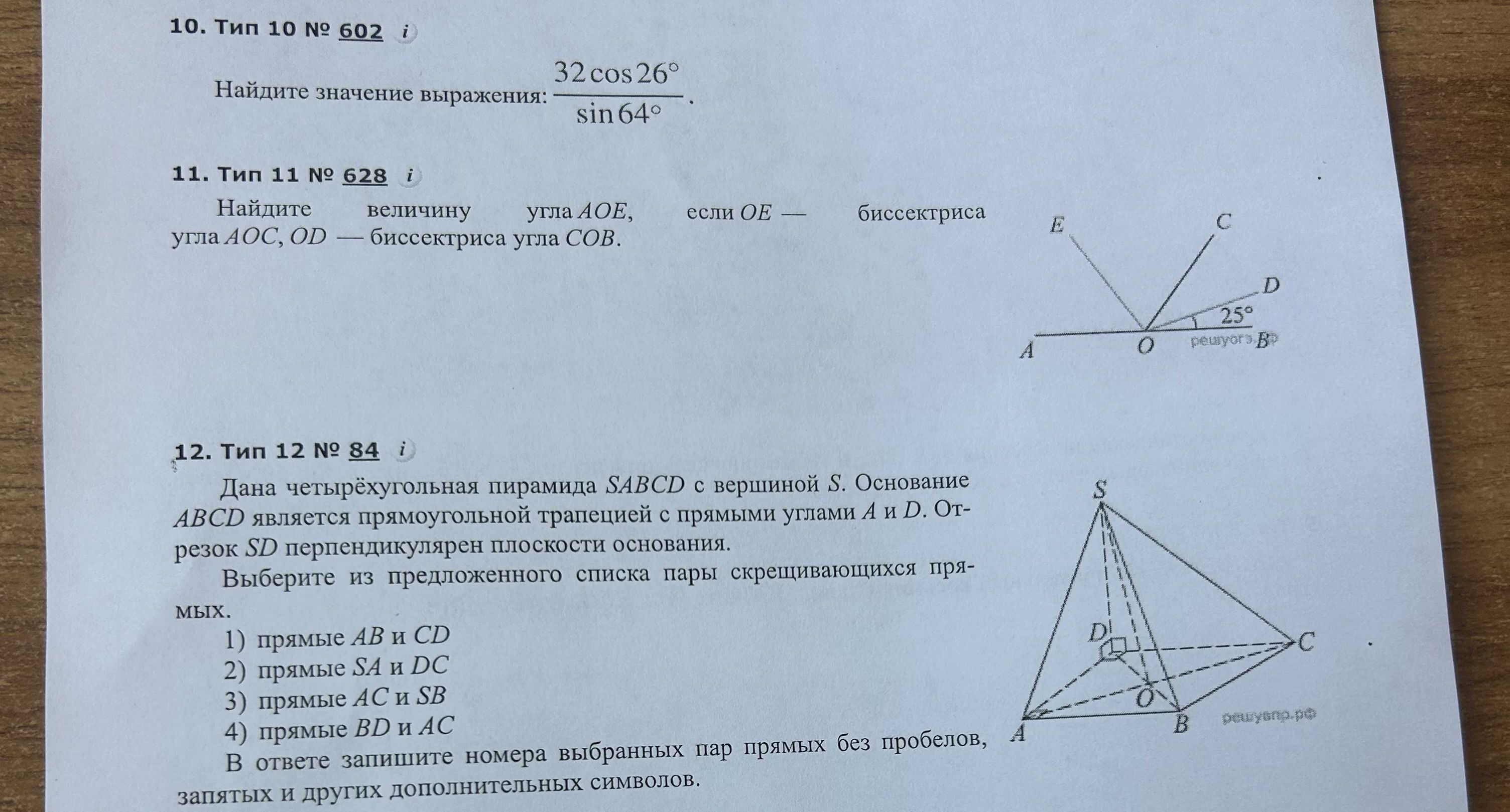
11. Найдите величину угла \(AOE\), если \(OE\) – биссектриса угла \(COB\). Найдите величину угла \(AOC\), \(OD\) – биссектриса угла \(COB\).

На рисунке видно, что угол \(BOD = 25^\circ\), так как \(OD\) – биссектриса угла \(COB\), то \(COB = 2 cdot BOD = 2 cdot 25^\circ = 50^\circ\). Угол \(AOC\) является смежным с углом \(COB\), значит, их сумма равна \(180^\circ\). Следовательно, \(AOC = 180^\circ - COB = 180^\circ - 50^\circ = 130^\circ\). Так как \(OE\) – биссектриса угла \(COB\), то \(COE = \frac{1}{2} COB = \frac{1}{2} cdot 50^\circ = 25^\circ\). Угол \(AOE\) можно найти как сумму углов \(AOC\) и \(COE\): \(AOE = AOC - COE = 130^\circ - 25^\circ = 105^\circ\). Ответ: \(AOC = 130^\circ\), \(AOE = 155^\circ\)