Вопрос:
Найдите сумму четырёх первых членов геометрической прогрессии (bn) со знаменателем q, если: b3=36, b6=1/6.
Ответ:
\[b_{3} = 36;\ \ b_{6} = \frac{1}{6}:\]
\[\left\{ \begin{matrix} b_{1}q^{2} = 36 \\ b_{1}q^{5} = \frac{1}{6}\text{\ \ } \\ \end{matrix} \right.\ \]
\[q^{3} = \frac{1}{36 \cdot 6}\text{\ \ }\]
\[q^{3} = \frac{1}{6^{3}}\ \]
\[q = \frac{1}{6}.\]
\[b_{1} = \frac{36 \cdot 36}{1} = 1296.\]
\[S_{4} = \frac{1296 \cdot \left( \frac{1}{1296} - 1 \right)}{\frac{1}{6} - 1} =\]
\[= \frac{1296 \cdot \left( - \frac{1295}{1296} \right)}{- \frac{5}{6}} =\]
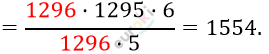
Похожие
- Геометрическая прогрессия (bn) задана формулой n–го члена bn=0,4*3^n-1. Найдите сумму пяти первых её членов.
- Найдите первый член геометрической прогрессии, если её знаменатель равен 1/4, а сумма четырёх первых членов равна 765.
- Найдите сумму четырёх первых членов геометрической прогрессии (bn) со знаменателем q, если: b1=корень из 3, b5=9*корень из 3, q>0.