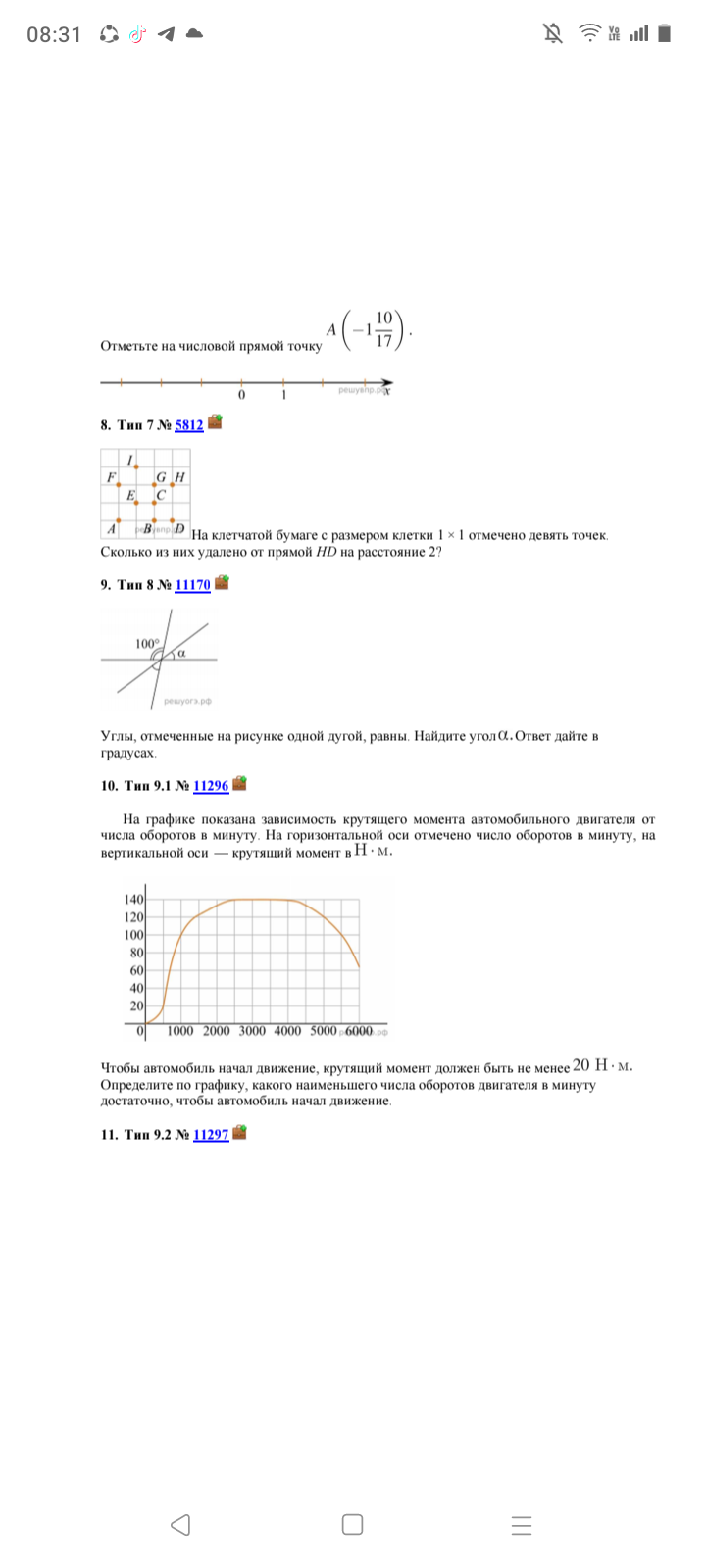
На клетчатой бумаге с размером клетки $1 \times 1$ отмечено девять точек. Сколько из них удалено от прямой $HD$ на расстояние 2?

На клетчатой бумаге отметим точки $A, B, C, D, E, F, G, H, I$. Необходимо найти точки, расстояние от которых до прямой $HD$ равно 2. Расстояние от точки до прямой измеряется по перпендикуляру. Прямая $HD$ проходит вертикально через точки $H$ и $D$. Точки $A, B, C, D, E, F, G, H, I$ имеют следующие координаты, если принять точку $A$ за начало координат (0,0): $A(0, 0), B(1, 0), C(1, 1), D(1, 2), E(0, 1), F(0, 2), G(2, 1), H(2, 2), I(0, 2)$. Прямая $HD$ имеет координату $x = 2$. Расстояние от любой точки до этой прямой равно $|x - 2|$, где $x$ - координата точки. - $A$: $|0 - 2| = 2$ - $B$: $|1 - 2| = 1$ - $C$: $|1 - 2| = 1$ - $D$: $|1 - 2| = 1$ - $E$: $|0 - 2| = 2$ - $F$: $|0 - 2| = 2$ - $G$: $|2 - 2| = 0$ - $H$: $|2 - 2| = 0$ - $I$: $|0 - 2| = 2$ Точки $A, E, F, I$ удалены от прямой $HD$ на расстояние 2. Всего 4 точки.