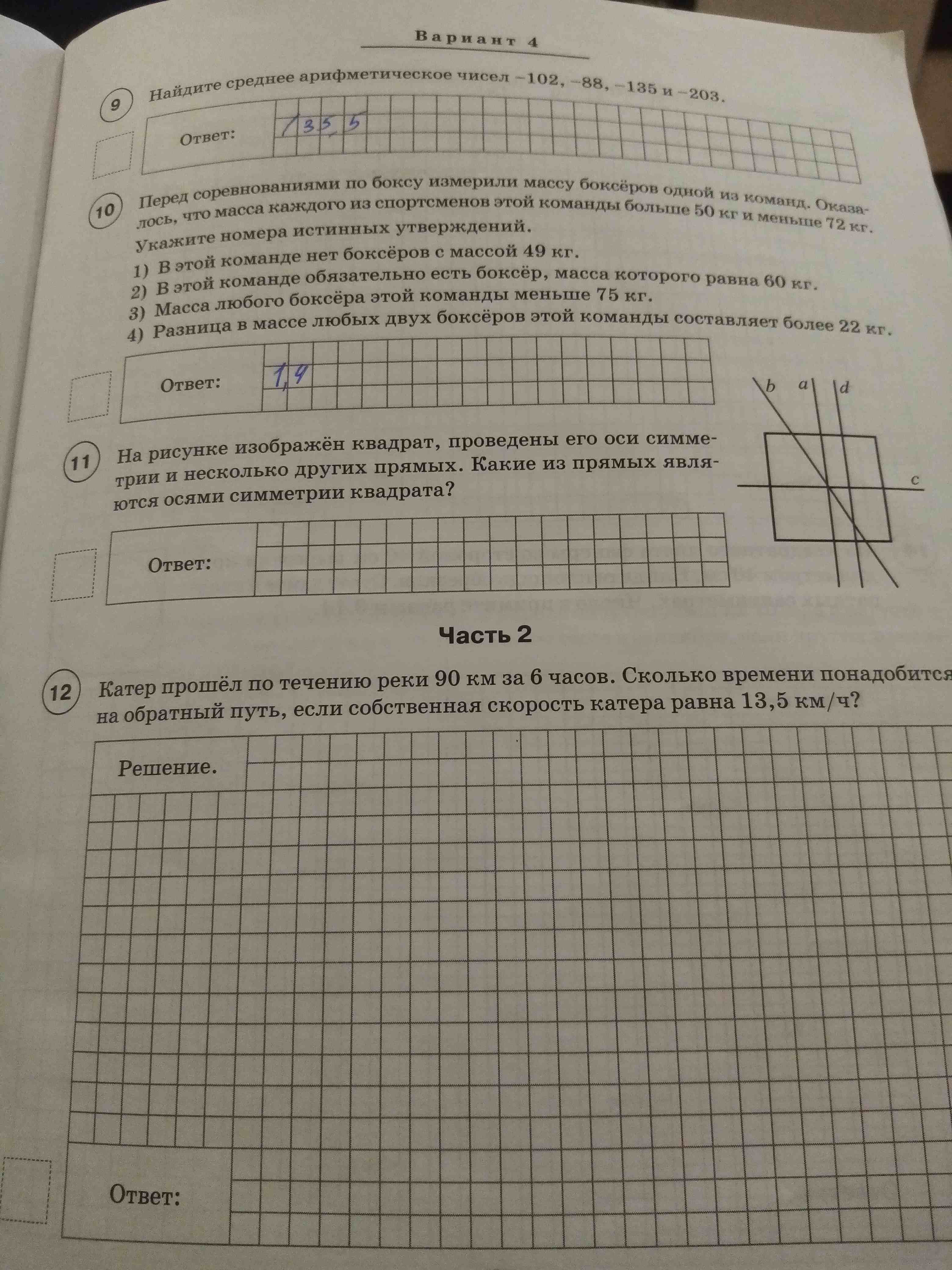
12) Катер прошёл по течению реки 90 км за 6 часов. Сколько времени понадобится на обратный путь, если собственная скорость катера равна 13,5 км/ч?

1. Найдем скорость катера по течению реки: \[v_{по течению} = \frac{S}{t} = \frac{90}{6} = 15 \text{ км/ч}\] 2. Найдем скорость течения реки: Пусть \(v_{соб} \) - собственная скорость катера, \(v_{теч} \) - скорость течения реки. Тогда: \[v_{по течению} = v_{соб} + v_{теч}\] Отсюда: \[v_{теч} = v_{по течению} - v_{соб} = 15 - 13,5 = 1,5 \text{ км/ч}\] 3. Найдем скорость катера против течения реки: \[v_{против течения} = v_{соб} - v_{теч} = 13,5 - 1,5 = 12 \text{ км/ч}\] 4. Найдем время, которое понадобится на обратный путь: \[t_{обратно} = \frac{S}{v_{против течения}} = \frac{90}{12} = 7,5 \text{ часов}\] Ответ: 7,5 часов