Исследуйте функцию: y=f(x), где f(x)=(2x)^3-5, монотонность. Используя результат исследования, сравните f(-корень из 6) и f(-2,4).

\[f(x) = 2x^{3} - 5;\ \ \ \ \ \ \ \]

\[\ x_{2} = x_{1} + \mathrm{\Delta};\ \ \ \ \ \ \ \mathrm{\Delta} \geq 0;\ \ \ \ x_{2} > x_{1}\]

\[f(x_{2}) - f(x_{1}) \geq 0\]

\[2 \cdot \left( x_{1} + \mathrm{\Delta} \right)^{3} - 5 - 2 \cdot \left( x_{1}^{3} \right) - 5 =\]

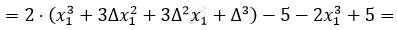
\[= 6\mathrm{\Delta}x_{1}^{2} + 3\mathrm{\Delta}^{2}x_{1} + x^{3} \geq 0;\ \ \ \ \ \]

\[\text{\ \ \ }(\mathrm{\Delta} \geq 0).\]

\[То\ есть\ \ f(x) - монотонно\ \]

\[возрастает;\ \ тогда:\ \]

\[f\left( - \sqrt{6} \right) < f( - 2,4).\]