Найдите наименьшее значение функции: y=11+корень из (5x^2-4x-12) и определите, при каких значениях x оно достигается.

\[y = 11 + \sqrt{5x^{2} - 4x - 12}\]

\[имеет\ y_{\min}\text{\ \ \ }при\text{\ \ }\]

\[5x^{2} - 4x - 12 = 0\]

\[D = 16 + 240 = 256\]

\[x_{1},_{2} = \frac{4 \pm 16}{10} = 2;\ \ - 1,2\]

\[y_{\min} = 11\]

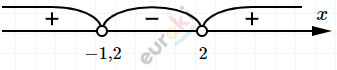
\[Ответ:\ \ \ y_{\min} = 11\ \ при\ \ x = 2;\]

\[\ \ x = - 1,2.\]