Две бригады при совместной работе могут выполнить задание за 15 дней. За сколько дней могла бы выполнить это задание каждая бригада в отдельности, если первой бригаде на выполнение всего задания потребуется на 40 дней больше, чем второй?

\[Пусть\ x\ дней - надо\ второй\ \]

\[бригаде;\]

\[(x + 40)\ дней - надо\ первой\ \]

\[бригаде.\]

\[Известно,\ что\ две\ бригады,\]

\[\ работая\ совместно,\ могут\ \]

\[выполнить\ работу\]

\[за\ 15\ дней.\]

\[Составим\ уравнение:\]

\[\frac{1^{\backslash 15x}}{x + 40} + \frac{1^{\backslash 15(x + 40(}}{x} = \frac{1^{\backslash x(x + 40)}}{15}\]

\[15x + 15 \cdot (x + 40) = x(x + 40)\]

\[15x + 15x + 600 = x^{2} + 40x\]

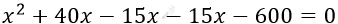
\[x^{2} + 10x - 600 = 0\]

\[x_{1} = 20\ (дней) - надо\ второй\ \]

\[бригаде.\ \ \ \ \]

\[x_{2} = - 30\ (не\ подходит)\]

\[x + 40 = 20 + 40 = 60\ (дней) -\]

\[надо\ первой\ бригаде.\]

\[Ответ:\ \ 60\ дней\ и\ 20\ дней.\]