Два туриста вышли одновременно из городов A и B навстречу друг другу и после встречи каждый продолжил движение в первоначальном направлении. Один из них, скорость которого на 3 км/ч больше скорости другого, прибыл в город A через 2 ч после встречи, а другой в город B – через 4 ч 30 мин после встречи. Найдите скорость каждого туриста. Через какое время после начала движения состоялась их встреча?

Ответ:

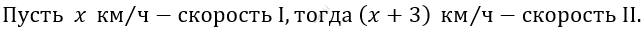
\[Пусть\ время\ встречи\ \ Т.\ \]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} T(x + 3) = 4,5x \\ Tx = 2 \cdot (x + 3) \\ \end{matrix}\text{\ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} Tx + 3T = 4,5x \\ Tx = 2x + 6\ \ \ \ \ \ \\ \end{matrix}\text{\ \ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} T = \frac{4,5x}{x + 3}\text{\ \ \ } \\ T = \frac{2x + 6}{x} \\ \end{matrix} \right.\ \]

\[\frac{4,5x}{x + 3} = \frac{2x + 6}{x}\]

\[4,5x² = (2x + 6)(x + 3)\]

\[4,5x² - 2x^{2} - 6x - 6x - 18 = 0\]

\[2,5x^{2} - 12x - 18 = 0\ \ \ \ \ \ \ | \cdot 2\]

\[5x^{2} - 24x - 36 = 0\]

\[D = 576 + 720 = 1296\ \ \ \]

\[x = \frac{24 - 36}{10} =\]

\[= - \frac{12}{10} - не\ удовлетворяет.\]

\[x = \frac{24 + 36}{10} = 6\]

\[6\ \frac{км}{ч - скорость\ \text{I\ }туриста.}\]

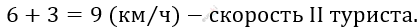
\[\frac{2 \cdot 6 + 6}{6} = 3\ (ч) - время,\ \]

\[через\ которое\ они\ \ встретятся.\]

\[Ответ:6\ \frac{км}{ч\ ;\ 9\frac{км}{ч;\ 3\ ч.}}\]