Дорога длиной 30 км, соединяющая село и железнодорожную станцию, идёт сначала с горы, а затем вверх. Из села на станцию велосипедист едет 2 ч 12 мин, а со станции – 2 ч 18 мин. С какой скоростью велосипедист едет с горы и с какой в гору, если его скорость на подъёме на 3 км/ч меньше его скорости на спуске?

Ответ:

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[катера;через\ t\ ч\ он\ догнал\ \]

\[плот,\ а\]

\[\left( t + 3 + 11\frac{40}{60} \right) =\]

\[= \left( t + 14\frac{2}{3} \right)\ ч - догнал\ лодку.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} tx = (t + 3) \cdot 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \left( t + \frac{33}{3} \right)x = \left( t + \frac{44}{3} \right) \cdot 24\ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} tx = 3t + 9\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ tx + \frac{35}{3}x = 24t + \frac{44 \cdot 24}{3} \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix} x = \frac{3t + 9}{t}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ 3tx + 35x - 72t - 1056 = 0 \\ \end{matrix} \right.\ \]

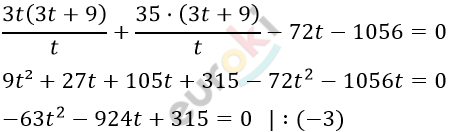
\[21t^{2} + 308t - 105 = 0\]

\[D = 94\ 864 + 8820 =\]

\[= 103\ 684 = 322^{2}\]

\[t = \frac{- 308 + 322}{42} = \frac{1}{3}\ (ч) -\]

\[время\ встречи\ с\ плотом.\]

\[t = \frac{- 308 - 322}{42} < 0.\]

\[x = \frac{3 \cdot \frac{1}{3} + 9}{\frac{1}{3}} = 30\ \left( \frac{км}{ч} \right) -\]

\[скорость\ катера.\]

\[Ответ:\ 30\frac{км}{ч}.\]