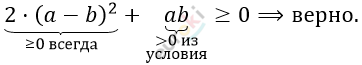Алгебра
Английский
Биология
География
Геометрия
Русский
История
Обществознание
Физика
Химия
Информатика
Литература
МатематикаВопрос:
Докажите, что: (a+2b)(1/2a+1/b)>=4, если a>0 и b>0.
Ответ:
\[(a + 2b)\left( \frac{1}{2a} + \frac{1}{b} \right) \geq 4,\]
\[a > 0\ \ и\ \ b > 0\]
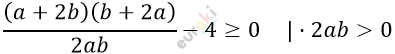
\[ab + 2a^{2} + 2b^{2} + 4ab - 8ab \geq 0\]
\[2a^{2} + 2b^{2} - 2ab + ab \geq 0\]
Похожие
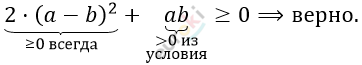
\[(a + 2b)\left( \frac{1}{2a} + \frac{1}{b} \right) \geq 4,\]
\[a > 0\ \ и\ \ b > 0\]
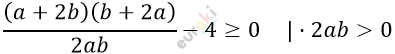
\[ab + 2a^{2} + 2b^{2} + 4ab - 8ab \geq 0\]
\[2a^{2} + 2b^{2} - 2ab + ab \geq 0\]