Автобус должен был проехать 280 км. Проехав 3/7 этого расстояния, автобус увеличил свою скорость на 20 км/ч. Найдите скорость автобуса на каждом участке движения, если на весь путь было затрачено 4 ч.

Ответ:

\[Пусть\ x\frac{км}{ч} - была\ скорость\ \]

\[автобуса;\ \]

\[\frac{3}{7} \cdot 280 = 120\ км - проехал\ \]

\[с\ этой\ скоростью.\ \]

\[(x + 20)\ \frac{км}{ч} - стала\ \]

\[скорость\ автобуса\ после\ \]

\[увеличения;\]

\[\ 280 - 120 = 160\ км - проехал\ \]

\[с\ новой\ скоростью.\]

\[На\ весь\ путь\ автобус\ \]

\[затратил\ 4\ часа.\]

\[Составим\ уравнение:\ \]

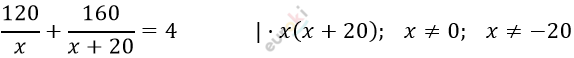
\[120 \cdot (x + 20) + 160x =\]

\[= 4x(x + 20)\]

\[120x + 2400 + 160x =\]

\[= 4x^{2} + 80x\]

\[280x + 2400 - 4x^{2} - 80x = 0\]

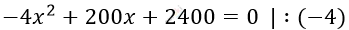
\[x^{2} - 50x - 600 = 0\]

\[x_{1} + x_{2} = 50;\ \ \ x_{1} \cdot x_{2} = - 600\]

\[x_{1} = 60\ \left( \frac{км}{ч} \right) -\]

\[первоначальная\ скорость\ \]

\[автобуса.\ \ \]

\[x_{2} = - 10\ \ (не\ подходит).\]

\[x + 20 = 60 + 20 =\]

\[= 80\ \left( \frac{км}{ч} \right) - скорость\ \]

\[автобуса\ после\ увеличения.\]

\[Ответ:60\frac{км}{ч};\ 80\ \frac{км}{ч}\text{.\ }\]