Средняя скорость. Средняя путевая скорость | Конспект

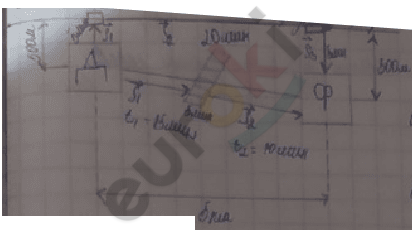
Сестра: \(t_{ср.}\) = 0,5 ч

\(\overrightarrow{S}\) = \({\overrightarrow{S}}_{1}\)+ \({\overrightarrow{S}}_{2}\) + \({\overrightarrow{S}}_{3}\) = 5 км

Брат: \(t_{ср.}\) = 0,5 ч

\(\overrightarrow{S}\) = \({\overrightarrow{S}}_{1}\)+ \({\overrightarrow{S}}_{2}\) = 5 км

\({\overrightarrow{v}}_{ср.}\) = \(\frac{{\overrightarrow{S}}_{общ.}}{t}\) – средняя скорость

Средней скоростью на данном участке траектории называется физическая величина, равная отношению перемещения тела на этом участке ко времени, за которое оно произошло.

\({\overrightarrow{v}}_{ср.}\) = \(\frac{5\ км}{0,5\ ч}\) = 10 км/ч

\(\overrightarrow{v}\) = 5 км на восток

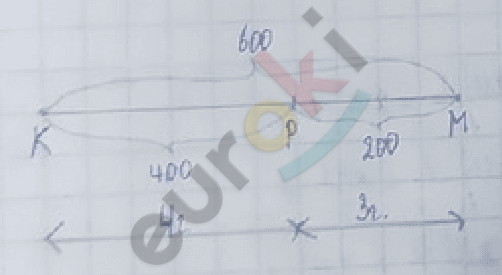
\(v_{ср.\ \ КР}\) = \(\frac{400}{4}\) = 100 км/ч

\(v_{ср.\ \ РМ}\) = \(\frac{200}{3}\) = 66,7 км/ч

\(v_{ср.\ \ КМ}\) = \(\frac{600}{7}\) = 85,7 км/ч

\(v_{ср.}\) = \(\frac{400}{7}\) = 57,1 км/ч

Если средняя скорость высчитывается по формуле \(\frac{{\overrightarrow{L}}_{общ.}}{t}\) = \(v_{ср.}\) и привязана к траектории, то такая скорость называется средняя путевая скорость.

\(\mathrm{\Delta}\)t → 0 → мгновенная скорость

Тело движется в плоскости

Построить траекторию частицы А (2; 1)

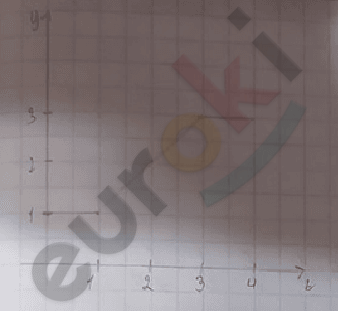
\(y_{0}\) = 1

\(v_{x}\) = \(\frac{y(t) - y_{0}}{t}\)

1) 0 = \(\frac{y(t)}{1}\) => \(y(t)\) = 1

2) 1 = \(\frac{y(t) - 1}{2}\) => \(y(t)\) = 3

3) 0 = \(\frac{y(t) - 3}{1}\) => \(y(t)\) = 3