Решебник по математике 6 класс Дорофеев контрольные работы КР-2. Десятичные дроби. Прямые на плоскости и в пространстве Вариант 4

1. Запишите числа:

а) 1 16/100 и 428/10000 в виде десятичных дробей;

б) 0,083 и 6,9 в виде обыкновенных дробей.

2. Запишите координаты точек А и С.

3. Используя десятичные дроби, выразите: а) 2060 кг в тоннах; б) 5 см в метрах.

4. Представьте числа 4/5 и 9/20 в виде десятичных дробей.

5. Запишите в порядке убывания числа 1,01; 0,91; 1,101.

6. Сравните числа 2/5 и 0,6.

7. Начертите прямые а и b, если известно, что один из углов, образовавшихся при их пересечении, равен 75°. Запишите величины трёх других углов.

8. а) Проведите прямую а (не по линиям сетки). На прямой а отметьте точку С. Через точку С проведите прямую b, перпендикулярную прямой а.

б) Отметьте точку D, не лежащую на прямых а и b. Измерьте и запишите расстояние от точки D до прямой b.

9. Даны числа 4/9, 3/4 и 0,4. Какое из них самое маленькое?

10. Даны две пары чисел, в которых некоторые цифры заменены звёздочкой: 3,*1 и 3,25; 2,95 и 2,*4.

В каком случае числа можно сравнить? Запишите соответствующее неравенство. Объясните письменно, почему другую пару чисел сравнить нельзя.

11. На прямой отмечены точки А, В, С и D так, что АВ = 5 см, ВС = 6 см, AD = 3 см и точка D лежит на отрезке ВС. Чему равна длина отрезка BD?

*12. Из цифр 1, 2, 3, 4 составляют всевозможные десятичные дроби с двумя знаками после запятой, при этом используют в записи дроби все четыре цифры, причём каждую только один раз. Сколько получится десятичных дробей, заключённых между числами 21 и 32?

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)}\ 1\frac{16}{100} = 1,16;\ \ \ \ \ \ \ \]

\[\frac{428}{10000} = 0,0428.\]

\[\textbf{б)}\ 0,083 = \frac{83}{1000};\ \ \ \ \ \]

\[6,9 = 6\frac{9}{10}.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[A(6,3);\ \ \ \ C(7,9).\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)}\ 2060\ кг = \frac{2060}{1000}\ т = 2,06\ т.\]

\[\textbf{б)}\ 5\ см = \frac{5}{100}\ м = 0,05\ м.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\frac{4}{5} = \frac{4 \cdot 20}{5 \cdot 20} = \frac{80}{100} = 0,8;\]

\[\frac{9}{20} = \frac{9 \cdot 5}{20 \cdot 5} = \frac{45}{100} = 0,45.\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[Числа\ в\ порядке\ убывания:\]

\[1,101;\ \ \ 1,01;\ \ 0,91.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[\frac{2}{5} = \frac{2}{10} = 0,2\]

\[0,2 < 0,6\]

\[\frac{2}{5} < 0,6.\]

\[\boxed{\mathbf{7}\mathbf{.}\mathbf{\ }}\]

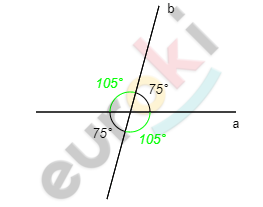
\[Ответ:\ \ 105{^\circ};\ \ \ 75{^\circ};\ \ 105{^\circ}.\]

\[\boxed{\mathbf{8}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)}\ a\bot b\]

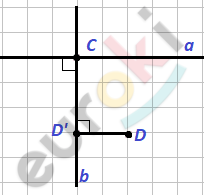
\[\textbf{б)}\ DD^{'} = 1\ см.\]

\[Ответ:\ \ DD^{'} = 1\ см.\]

\[\boxed{\mathbf{9}\mathbf{.}\mathbf{\ }}\]

\[\frac{4}{9} = 0,44\ldots\]

\[\frac{3}{4} = 0,75\]

\[0,4 < \frac{4}{9} < \frac{3}{4}.\]

\[Ответ:\ самое\ маленькое\ число\ 0,4.\]

\[\boxed{\mathbf{10}\mathbf{.}\mathbf{\ }}\]

\[Первую\ пару\ чисел\ сравнить\ нельзя,\]

\[потому\ что\ при*\ = 1;2\ будет\ один\]

\[знак,\ а\ при\ остальных\ значениях -\]

\[другой\ знак\ неравенства.\]

\[2,95 > 2,*4.\]

\[\boxed{\mathbf{11}\mathbf{.}\mathbf{\ }}\]

\[BD = 2\ см.\]

\[Ответ:\ \ BD = 2\ см.\]

\[\boxed{\mathbf{12}\mathbf{.}\mathbf{\ }}\]

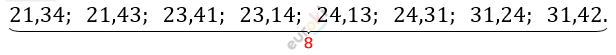
\[Ответ:8\ дробей.\]

## КР-3. Действия с десятичными дробями