Решебник по математике 6 класс Дорофеев контрольные работы КР-7. Рациональные числа Вариант 1

1. Начертите координатную прямую с единичным отрезком, равным 2 клеткам, отметьте на ней число 1,5 и противоположное ему число.

2. Найдите: |10|, |–0,7|, |0|.

3. Дополните равенства, записав без скобок данные выражения:

+(–15) = …; –(+60) = …; –(–45) = ….

4. Сравните числа:

а) –1,16 и –1,6;

б) 1/3 и –1 1/2.

5. Выполните действия:

а) 4/11-2/3

б) 9:(-1/3)

в) (-0,5)^3

6. Вычислите:

а) -1,5+5-2,5

б) -10-6*1,5

7. Найдите значение выражения –4а при а = 5/8.

8. Постройте прямоугольную систему координат, отметьте точки А(–4; 3) и В(4; –1), соедините их отрезком. Запишите координаты точки, в которой отрезок АВ пересекает ось у.

9. Найдите значение выражения (0,8-1,6)/(-1,2-0,6).

10. Запишите все целые числа, модуль которых меньше 5.

11.Сравните с нулем:

(-4,83)^3;

(-0,062)^4.

12. Найдите неизвестное число х: –(–(–(–x))) = 15. Запишите своё решение.

\[\boxed{\mathbf{Вариант}\mathbf{\ 1}\mathbf{.}\mathbf{\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[|10| = 10\]

\[| - 0,7| = 0,7\]

\[|0| = 0\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[+ ( - 15) = - 15\]

\[- ( + 60) = - 60\]

\[- ( - 45) = 45\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)} - 1,16 > - 1,6\]

\[\textbf{б)}\ \frac{1}{3} > - 1\frac{1}{2}\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)}\ \frac{4^{\backslash 3}}{11} - \frac{2^{\backslash 11}}{3} = \frac{12 - 22}{33} = - \frac{10}{33}\]

\[\textbf{б)}\ 9\ :\left( - \frac{1}{3} \right) = 9 \cdot ( - 3) = - 27\]

\[\textbf{в)}\ ( - 0,5)^{3} = - 0,125\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)} - 1,5 + 5 - 2,5 = 5 - 4 = 1\]

\[\textbf{б)} - 10 - 6 \cdot 1,5 = - 10 - 9 =\]

\[= - (10 + 9) = - 19\]

\[\boxed{\mathbf{7}\mathbf{.}\mathbf{\ }}\]

\[- 4a\]

\[при\ a = \frac{5}{8}:\]

\[- 4 \cdot \frac{5}{8} = - \frac{4 \cdot 5}{8} = - \frac{5}{2} = - 2,5.\]

\[Ответ:\ - 2,5.\]

\[\boxed{\mathbf{8}\mathbf{.}\mathbf{\ }}\]

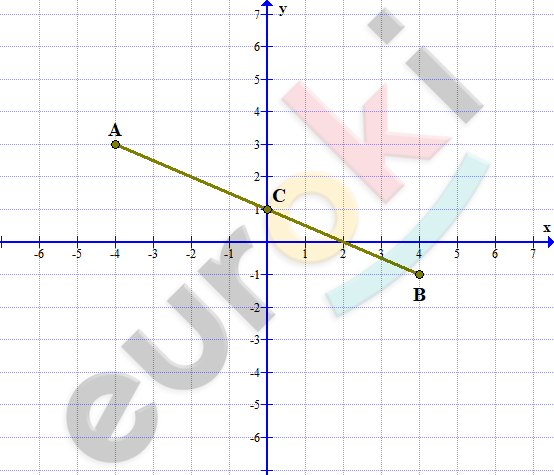
\[C(0;1).\]

\[\boxed{\mathbf{9}\mathbf{.}\mathbf{\ }}\]

\[\frac{0,8 - 1,6}{- 1,2 - 0,6} = \frac{- 0,8}{- 1,8} = \frac{8}{18} = \frac{4}{9}\]

\[Ответ:\ \frac{4}{9}.\]

\[\boxed{\mathbf{10}\mathbf{.}\mathbf{\ }}\]

\[|x| < 5\]

\[- 5 < x < 5\]

\[x = - 4;\ - 3;\ - 2;\ - 1;\ \ 1;\ \ \]

\[= 2;\ \ 3;\ \ 4.\]

\[\boxed{\mathbf{11}\mathbf{.}\mathbf{\ }}\]

\[( - 4,58)^{3} < 0\ \ \ \ \ \]

\[( - 0,062)^{4} > 0\]

\[\boxed{\mathbf{12}\mathbf{.}\mathbf{\ }}\]

\[Первый\ способ:\ \]

\[- \left( - \left( - ( - x) \right) \right) = 15\]

\[- \left( - ( - x) \right) = - 15\]

\[- ( - x) = 15\]

\[- x = - 15\]

\[x = 15\]

\[Второй\ способ\ (проще):\]

\[так\ как\ количество\ знаков\ « - »\]

\[четное,\ то\ получаем\]

\[+ x = 15\]

\[x = 15.\]

\[Ответ:15.\]