Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 994
Задание 994
\[\boxed{\mathbf{994.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Дано:}\]
\[\textbf{а)}\ D(1;1);A(5;4);\]
\[B(4; - 3);C( - 2;5).\]
\[\textbf{б)}\ D(1;0);A(7; - 8);\]
\[B( - 5;8);C(9;6).\]
\[\mathbf{Доказать:}\]
\[AD = DB = DC.\]
\[\mathbf{Доказательство.}\]
\[\textbf{а)}\ 1)\ AD =\]
\[= \sqrt{(5 - 1)^{2} + (4 - 1)^{2}} =\]
\[= \sqrt{25} = 5;\]
\[2)\ DB = \sqrt{(1 - 4)^{2} + (1 + 3)^{2}} =\]
\[= \sqrt{25} = 5;\]
\[3)\ DC = \sqrt{(1 + 2)^{2} + (1 - 5)^{2}} =\]
\[= \sqrt{25} = 5;\]
\[4)\ AD = DB = DC = 5.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ 1)\ AD =\]
\[= \sqrt{(7 - 1)^{2} + ( - 8 - 0)^{2}} =\]
\[= \sqrt{100} = 10;\]
\[2)\ DB = \sqrt{(1 + 5)^{2} + (0 - 8)^{2}} =\]
\[= \sqrt{100} = 10;\]
\[3)\ DC = \sqrt{(1 - 9)^{2} + (0 - 6)^{2}} =\]
\[= \sqrt{100} = 10;\]
\[4)\ AD = DB = DC = 10.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{994.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
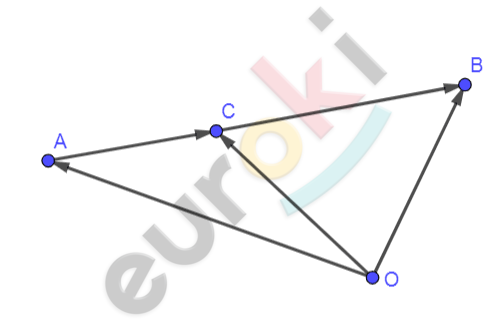
\[\mathbf{Дано:}\]
\[AB - отрезок;\]
\[C \in AB;\ \ \]
\[AC\ :CB = m\ :n;\]
\[( \bullet )O - любая.\]
\[\mathbf{Доказать:}\]
\[\overrightarrow{\text{OC}} = \frac{n}{m + n}\overrightarrow{\text{OA}} + \frac{m}{m + n}\overrightarrow{\text{OB}}.\]
\[\mathbf{Доказательство.}\]
\[1)\frac{\text{AC}}{\text{CB}} = \frac{m}{n}\]
\[AC \bullet n = CB \bullet m.\ \]
\[\overrightarrow{\text{AC}} = \frac{m}{n}\overrightarrow{\text{CB}}.\]
\[2)\ По\ правилу\ треугольника:\]
\[\overrightarrow{\text{OC}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{AC}}.\]
\[3)\ \overrightarrow{\text{AC}} = \frac{m}{n}\overrightarrow{\text{CB}} = \frac{m}{n}\left( \overrightarrow{\text{OB}} - \overrightarrow{\text{OC}} \right).\]
\[4)\ \overrightarrow{\text{OC}} = \overrightarrow{\text{OA}} + \frac{m}{n}\left( \overrightarrow{\text{OB}} - \overrightarrow{\text{OC}} \right) =\]
\[= \overrightarrow{\text{OA}} + \frac{m}{n}\overrightarrow{\text{OB}} - \frac{m}{n}\overrightarrow{\text{OC}}\]
\[\overrightarrow{\text{OC}} + \frac{m}{n}\overrightarrow{\text{OC}} = \overrightarrow{\text{OA}} + \frac{m}{n}\overrightarrow{\text{OB}}\]
\[\overrightarrow{\text{OC}} = \frac{n}{m + n}\overrightarrow{\text{OA}} + \frac{m}{m + n}\overrightarrow{\text{OB}}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
