Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 903
Задание 903
\[\boxed{\mathbf{903.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Докажите\ утверждения\ об\ \]
\[основных\ свойствах\ \]
\[умножения\ вектора\ на\ число\ \]
\[(п.\ 86).\]
\[Доказательство.\]
\[1)\ Докажем,\ что\ для\ любых\ \]
\[чисел\ \text{k\ }и\ \text{l\ }и\ любого\ вектора\ \overrightarrow{a}\ \]
\[справедливо\ равенство:\]
\[\left( \text{kl} \right)\overrightarrow{a} = l\left( l\overrightarrow{a} \right)\]
\[2)\ Если\ \overrightarrow{a} = \overrightarrow{0} \Longrightarrow\]
\[\Longrightarrow справедливость\ равенства\ \]
\[очевидна.\]
\[3)\ Если\ \overrightarrow{a} \neq \overrightarrow{0}:\]
\[\left| \left( \text{kl} \right)\overrightarrow{a} \right| = \left| \text{kl} \right|\left| \overrightarrow{a} \right| = |k||l|\left| \overrightarrow{a} \right| =\]
\[= |k|\left| l\overrightarrow{a} \right| = \left| k\left( l\overrightarrow{a} \right) \right|.\]
\[Если\ kl \geq 0:\]
\[\ \left( \text{kl} \right)\overrightarrow{a} \uparrow \uparrow \overrightarrow{a}\ и\ k\left( l\overrightarrow{a} \right) \uparrow \uparrow \overrightarrow{a}.\]
\[Если\ kl < 0:\]
\[\left( \text{kl} \right)\overrightarrow{a} \uparrow \downarrow \overrightarrow{a};\ \]
\[k\left( l\overrightarrow{a} \right) \uparrow \downarrow \overrightarrow{a}.\]
\[Следовательно:\ \left( \text{kl} \right)\overrightarrow{a} = l\left( l\overrightarrow{a} \right).\]
\[Что\ и\ требовалось\ доказать.\]
\[4)\ Докажем,\ что\ для\ любых\ \]
\[чисел\ \text{k\ }и\ любых\ векторов\ \overrightarrow{a}\ и\ \overrightarrow{b}\ \]
\[справедливо\ равенство:\ \]
\[k\left( \overrightarrow{a} + \overrightarrow{b} \right) = k\overrightarrow{a} + k\overrightarrow{b}.\]
\[5)\ Если\ k = 0 \Longrightarrow\]
\[\Longrightarrow справедливость\ равенства\ \]
\[очевидна.\]
\[6)\ При\ k \neq 0\ и\ если\ \overrightarrow{a}\ и\ \overrightarrow{b} - не\ \]
\[коллинеарны.\]
\[Отложим\ от\ какой\ нибудь\ \]
\[точки\ O\ векторы\ \overrightarrow{OA_{1}} =\]
\[= \overrightarrow{a}\ и\ \overrightarrow{\text{OA}} = k\overrightarrow{a},\ а\ от\]
\[точек\ A_{1}\ и\ A_{2} - векторы\ \]
\[\overrightarrow{A_{1}B_{1}} = \overrightarrow{b}\ и\ \overrightarrow{\text{AB}} = k\overrightarrow{b}.\]
\[Треугольника\ OA_{1}B_{1}\ и\ \]
\[OAB - подобны,\ с\ \]
\[коэффициентом\ подобия\ |k|.\]
\[Следовательно:\ \]
\[\overrightarrow{\text{OB}} = k\overrightarrow{OB_{1}} = k\left( \overrightarrow{a} + \overrightarrow{b} \right);\]
\[\overrightarrow{\text{OB}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{AB}} = k\overrightarrow{a} + k\overrightarrow{b}.\]
\[Отсюда:\]
\[k\left( \overrightarrow{a} + \overrightarrow{b} \right) = k\overrightarrow{a} + k\overrightarrow{b}.\]
\[Что\ и\ требовалось\ доказать.\]
\[7)\ (k + l)\overrightarrow{a} = k\overrightarrow{a} + l\overrightarrow{a}.\]
\[8)\ Пусть\ хотя\ бы\ одно\ из\ чисел\ \]
\[\text{k\ }или\ l - отлично\ от\ нуля:\]
\[|k| \geq |l|,\ k \neq 0\ и\ \left| \frac{l}{k} \right| \leq 1.\]
\[9)\ Рассмотрим\ вектор\ \]
\[\overrightarrow{a} + \frac{l}{k}\overrightarrow{a} \Longrightarrow \overrightarrow{a} + \frac{l}{k}\overrightarrow{a} \uparrow \uparrow \overrightarrow{a};\]
\[\left| \overrightarrow{a} + \frac{l}{k}\overrightarrow{a} \right| = \left| \overrightarrow{a} \right| + \frac{l}{k}\left| \overrightarrow{a} \right| =\]
\[= \left( 1 + \frac{l}{k} \right)\left| \overrightarrow{a} \right|.\]
\[10)\ Следовательно:\ \ \]
\[\overrightarrow{a} + \frac{l}{k}\overrightarrow{a} = \left( 1 + \frac{l}{k} \right)\overrightarrow{a}\ | \bullet k\]
\[(k + l)\overrightarrow{a} = k\overrightarrow{a} + l\overrightarrow{a}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{903.еуроки - ответы\ на\ пятёрку}}\]
\[Дано:\]
\[окружность;\]
\[AB = CD - хорды.\]
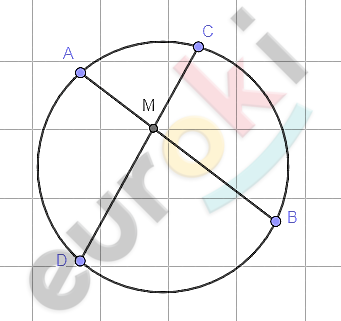
\[Доказать:\]
\[AM = CM;\]
\[BM = MD.\]
\[Доказательство.\]
\[1)\ Если\ точка\ перемечения\ \]
\[лежит\ внутри\ круга,\ то\ по\ \]
\[теореме\ п.1:\ \ \]
\[AM \bullet MB = CM \bullet MD.\]
\[2)\ AB = CD:\]
\[MB = AB - AM;\]
\[MD = AB - CM.\]
\[Тогда:\]
\[AM \bullet (AB - AM) =\]
\[= CM \bullet (AB - CM);\]
\[AM = CM;\ \ \]
\[BM = AB - AM = AB - CM =\]
\[= \text{MD.}\]
\[Что\ и\ требовалось\ доказать.\]
\[3)\ Если\ точка\ пересечения\ \]
\[находится\ вне\ круга,\ то\ по\ \]
\[теореме\ п.\ 2:\ \ \]
\[MA \bullet MB = MK^{2}\text{\ \ }и\ \ MC \bullet CD =\]
\[= MK^{2}\]
\[MA \bullet (AB - AM) =\]
\[= CM \bullet (AB - CM) = MK^{2}\]
\[MA = MC\ \ и\ \ MB = MD.\]
\[Что\ и\ требовалось\ доказать.\]
