Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 857
Задание 857
\[\boxed{\mathbf{857.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм.\]
\[\mathbf{Доказать:}\]
\[есть\ MNPQ - выпуклый\ \]
\[четырехугольник,\]
\[A;B;C;D - середины\ его\ \]
\[сторон.\]
\[\mathbf{Доказательство.}\]
\[1)\ Построим\ точку\ M - вне\ \]
\[параллелограмма\ \text{ABCD\ }\ \]
\[и\ не\ лежащую\ на\ прямых,\ \]
\[содержащих\ его\ стороны.\ \]
\[Получаем:\]
\[точка\ N - симметрична\ M\ \]
\[относительно\ ( \bullet )A;\]
\[точка\ P - симметрична\ \text{N\ }\]
\[относительное\ ( \bullet )B;\]
\[точка\ Q - симметрична\ \text{P\ }\]
\[относительно\ ( \bullet )\text{C.}\]
\[2)\ Надо\ доказать,\ что\ D \in MQ;\ \ \]
\[MD = DQ\ или\ \]
\[что\ ( \bullet )\text{M\ }симметрична\ ( \bullet )\text{Q\ }\]
\[относительно\ ( \bullet )\text{D.}\]
\[Достроим\ чертеж:проведем\ \]
\[диагональ\ \text{QN.}\]
\[3)\ Рассмотрим\ треугольник\ \]
\[QPN:\]
\[\text{BC\ }(сторона\ параллелограмма) -\]
\[средняя\ линия;\]
\[BC \parallel NQ.\ \]
\[Следовательно,в\ треугольнике\ \]
\[QMN:\]
\[AD \parallel BC \parallel NQ;\ \ \ \]
\[MA = AN.\]
\[4)\ Получаем:\]
\[AD - средняя\ линия\ \]
\[треугольника\ QMN;\]
\[MD = DQ.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{857.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
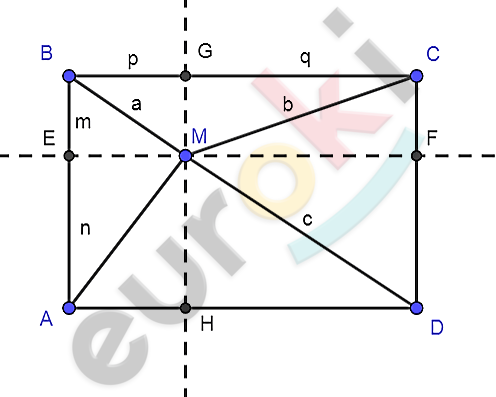
\[ABCD - прямоугольник;\]
\[MB = a;\ \ MC = b;\]
\[MD = c.\]
\[\mathbf{Найти:}\]
\[MA - ?\]
\[\mathbf{Решение.}\]
\[1)\ Проведем\ через\ ( \bullet )\text{M\ }\]
\[прямые\ EF \parallel AD;\ \ GH \parallel AB.\]
\[2)\ Пусть\ MA = x;\ \ \]
\[AE = HM = FD = m;\ \]
\[EB = MG = FC = n;\ \ \]
\[BG = EM = AH = p;\]
\[GC = MF = HD = q.\]
\[3)\ По\ теореме\ Пифагора:\]
\[a^{2} = n^{2} + p^{2};\]
\[b^{2} = n^{2} + q^{2}.\]
\[Получаем:\]
\[a^{2} + c^{2} = n^{2} + p^{2} + m^{2} + q^{2} =\]
\[= x^{2} + b^{2};\]
\[c^{2} = m^{2} + q^{2};\]
\[x^{2} = m^{2} + p^{2}.\]
\[4)\ x^{2} = a^{2} - b^{2} + c^{2}\]
\[x = \sqrt{a^{2} - b^{2} + c^{2}}.\]
\[Ответ:\ \sqrt{a^{2} - b^{2} + c^{2}}.\]
