Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 165
Задание 165
\[\boxed{\mathbf{165.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
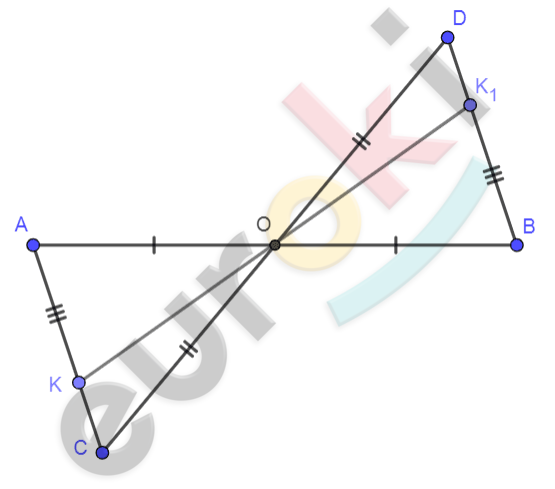
\[\mathbf{Дано:}\]
\[AB \cap CD = O;\]
\[AO = OB;OD = CO;\]
\[K \in AC;K_{1} \in DB;\]
\[AK = BK_{1}.\]
\[\mathbf{Доказать:}\]
\[\textbf{а)}\ OK = OK_{1};\]
\[\textbf{б)}\ O \in KK_{1}.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}AOC = \mathrm{\Delta}BOD - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[AO = OB\ (по\ условию);\]
\[CO = OD\ (по\ условию);\]
\[\angle AOC = \angle DOB\ \]
\[(как\ вертикальные).\]
\[Значит:\]
\[\angle A = \angle B.\]
\[2)\ \mathrm{\Delta}AKO = \mathrm{\Delta}BK_{1}O - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[AO = OB\ (по\ условию);\]
\[AK = BK_{1}\ (по\ условию);\]
\[\angle A = \angle B\ (см.\ пункт\ 1).\]
\[Следовательно:\ \]
\[KO = OK_{1}.\]
\[3)\ \angle AOK = \angle BOK_{1} - по\ \]
\[пункту\ 2;\]
\[AB - отрезок.\]
\(\ \) \(Получаем:\)
\[\angle\text{AOK\ \ }и\ \ \angle BOK_{1} -\]
\[вертикальные.\]
\[Отсюда:\ \ \]
\[KK_{1} - лежит\ на\ одной\ прямой\ \]
\[и\ точка\ O \in KK_{1}\ .\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{165.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[a\bot AB;\]
\[a \in AB = O.\]
\[\mathbf{Доказать:}\]
\[1)\ AD = DB;\]
\[2)\ если\ AD = DB;то\ D \in a.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}DOA = \mathrm{\Delta}\text{DOB} - \ по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[DO - общая\ сторона;\]
\[\angle DOA = \angle DOB = 90{^\circ}\ \]
\[(так\ как\ a\bot AB);\]
\[AO = OB\ (по\ условию).\]
\[Получаем:\ AD = DB.\]
\[2)\ \mathrm{\Delta}\ DOA = \mathrm{\Delta}DOB - по\ трем\ \]
\[сторонам:\ \]
\[DO - общая\ сторона;\]
\[AD = DB\ (по\ условию);\]
\[AO = OB\ (по\ условию).\]
\[Значит:\]
\[\ \angle ADO = \angle ODB;\ \ \]
\[\angle AOD = \angle DOB.\]
\[3)\ \angle AOD\ и\ \angle DOB - смежные\ \]
\[и\ равные\ (по\ пункту\ 2):\]
\[\angle AOD = \angle DOB = 90{^\circ}.\]
\[Следовательно:\]
\[DO\bot AB;\ \ OD\ и\ a - совпадают;\ \]
\[D \in a.\]
\[Что\ и\ требовалось\ доказать.\]
